Дифференцируемость функции

.

Механический смысл производной. Рассмотрим функцию , определенную и непрерывную в некоторой окрестности точки . Если аргумент функции получает приращение 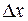(положительное или отрицательное), такое, что 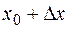принадлежит той же окрест­ности точки , то соответствующее приращение функции 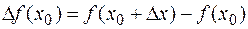, тогда средняя скорость изменения функции

,

а мгновенная скорость ее изменения

.

В этом состоит механический смысл производной, т. е. производная — математическая модель мгновенной скорости процесса, описываемого функцией . В зависимости от содержа­тельной сущности функции можно получить широкий круг математи­ческих моделей скорости протекания процессов. Рассмотрим некото­рые из них.

1. Пусть материальная точка движется неравномерно и — функция, устанавливающая зависимость пути от времени 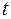. Тогда мгновенная скорость движения в момент времени есть произ­водная от пути по времени :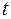

.

2. Пусть —функция, описывающая процесс изменения скорости неравномерного движения в зависимости от времени 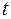. Тогда мгновенное ускорение материальной точки в фиксированный момент времени есть производная от скорости по времени :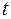

.

3. Пусть 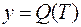— функция, описывающая процесс изменения количества теплоты, сообщаемой телу при нагревании его до темпе­ратуры 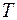. Тогда теплоемкость тела есть производная от количества теплоты 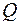по температуре :

.

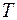Геометрический смысл производной. Рассмотрим задачу о прове­дении касательной к произвольной плоской кривой.

Определение. Касательной к кривой 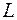в точке 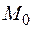называ­ется прямая , которая представляет собой предельное положение секущей 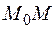при стремлении по кривой точки 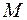к точке .

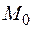Если предельного положения секущей не существует, то говорят, что в точке 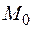провести касательную нельзя. Это бывает в случае, когда точка 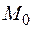является точкой излома, или заостре­ния, кривой.

Пусть кривая 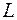является графиком функции и точка . Предположим, что касательная к кривой в точке 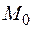существует. Угловой коэффициент секущей .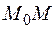

Если 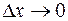, то точка 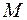движется по кривой к точке 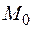и секущая 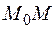стремится к своему предельному положению . Таким образом,

,

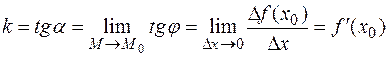т. е. если кривая 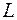является графиком функции, то производная от функции при равна угловому коэффици­енту касательной к графику функции в точке с абсциссой .

Уравнения касательной и нормали. Угол между кривыми. Для составления уравнений касатель­ной и нормали к плоской кривой используем геометрическую интер­претацию производной.

Пусть кривая задана уравнением . Угловой коэффициент касательной к ней в точк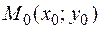е , где . . 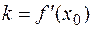Уравнение касательной можно найти, используя уравнение прямой, проходящей через данную точку в заданном направлении: , но 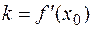поэтому

есть уравнение искомой касательной.

Так как угловые коэффициенты касательной и нормали связаны условием перпендикулярности 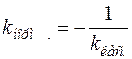, то уравнение норма­ли в точке 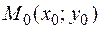имеет вид

.

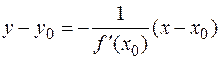Определение. Углом между кривыми называют угол между касательными к кривым в точке их пересечения.

Определение. Две линии называют ортогональ­ными, если они пересекаются под прямым углом.

Пример. Найти угол, под которым синусоида пересекает ось в начале координат.

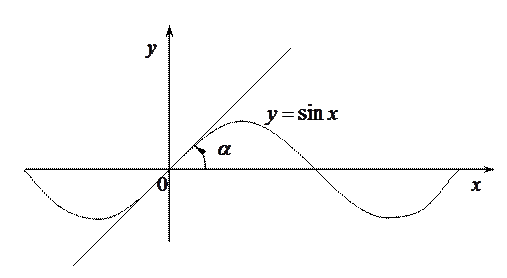
Решение. Так как , то 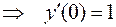, следовательно касательная, а значит, и синусоида, пересекают ось 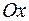под таким углом , для которого 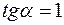, т. е. под углом .

Определение. Если для функции в точке существует предел

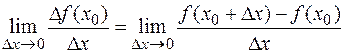, (1)

то говорят, что при данном значении функция дифференцируема

или (что равносильно этому) имеет производную.

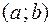Если функция дифференцируема в каждой точке некоторого отрезка (или интервала ), то гово­рят, что она дифференцируема на отрезке (или на интервале ).

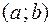Связь между непрерывностью и дифференцируемостью функции в данной точке устанавливает

Теорема. Если функция дифференцируема в некото­рой точке, то она и непрерывна в этой точке.

Доказательство. Действительно, если функция дифференцируема в точ­ке , то существует предел

,

Следовательно,

,

где ― бесконечно малая функция при .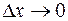

Умножим последнее равенство на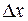

(2)

Тогда

что и означает (по определению 3) непрерывность функции в точке .

⊠

Утверждение, обратное данной теореме, вообще говоря, неверно, т. е. из непрерывности функции в точке еще не следует ее дифференцируемость в этой точке.

Например, рассмотрим функцию . Очевидно, что эта функция определена и непрерыв­на на 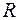. Но в точке не имеет производной, т.к. 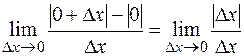не существует — не равны левосторонний и правосторонний пределы:

,

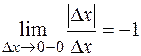Замечание. Так как равенство (1) равносильно равенству (2), то часто функцию называют дифференцируемой в точке , если ее приращение может быть представлено в виде (2).

Дата добавления: 2014-01-04