Правило Лопиталя

При раскрытии неопределенностей полезна следующая теорема, впервые доказанная И. Бернулли.

Теорема (правило Лопиталя). Если функции и 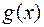удовлетворяют следующим условиям:

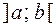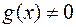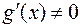
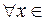
1) определены и дифференцируемы на интервале , причем и , за исклю­чением, быть может, точки ;

2) (либо );

3) существует предел (конечный или бесконечный) отношения производных

,

то существует также предел отношения функций 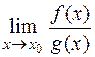, причем

.

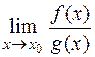
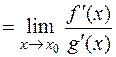Доказательство. Приведем доказательство теоремы только для случая раскры­тия неопределенностей вида . Доопределим функции и 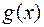в точке , положив . Доопределенные таким образом функции будут непрерывны в точке .

Рассмотрим отрезок |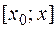, где 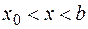. На этом отрезке функции и 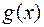непрерывны и дифференцируемы. Следовательно, по теореме Коши существует точка 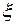(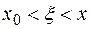) такая, что

.

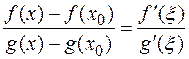Если 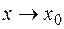, то и 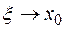, поэтому, согласно условию 3 теоремы, из последнего равенства следует, что

.

⊠

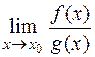
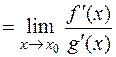Смысл правила Лопиталя заклю­чается в том, что оно позволяет свести вычисление предела отношения функции в случае неопределенности вида или 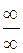к пределу отношения производных, который очень часто вычисляется проще.

Правило Лопиталя справедливо и в случае ¥.

Правило Лопиталя можно применять до тех пор, пока не будет получена дробь, для которой условия, предусмотренные теоремой, уже не выполняются.

Пример. Вычислить .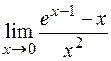

Решение. Непосредственная подстановка предельного значения 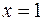при­водит к неопределенности вида . Для ее раскрытия применим правило Лопиталя:

.

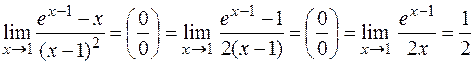Правило Лопиталя здесь применено дважды.

Замечание. Неправомерное применение правила Лопиталя, то есть если не выполняются условия теоремы может привести к неверному результату.

Дата добавления: 2014-01-04