Доказательство. Необходимость. Предположим, что — наклонная асимптота графика функции

Необходимость. Предположим, что — наклонная асимптота графика функции . Тогда справедливо представ­ление

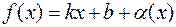, где при +¥.

Следовательно, .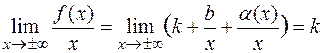

Достаточность. Пусть существуют данные пределы, тогда второе равенство означает, что при представимо в виде:

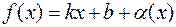, где при +¥,

то есть прямая является наклонной асимптотой графика функции .

Итак, теорема доказана для случая +¥. Доказательство теоре­мы для случая –¥ производится аналогично.

⊠

Замечание. При нахождении наклонных асимптот графика функции воз­можны следующие случаи: 1) оба предела существуют и не зависят от знака бесконечности, тогда прямая называется двусторонней асимптотой; 2) оба предела существуют, но при +¥ и –¥ они различны, тогда имеем две односто­ронние наклонные асимптоты; 3) если хотя бы один из пределов не существует, то наклонных асимптот нет.

Пример. Найти асимптоты линии .

Решение. Данная функция определена и непрерывна на , за исключением точки .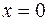

-¥, +¥.

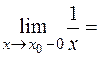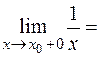Следовательно, 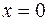является вертикальной асимптотой.

Для нахождения невертикальных асимптот вычисляем пределы

,

.

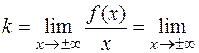
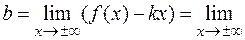
Получаем, что график функции имеет горизонтальную асимптоту

Пример. Найти асимптоты графика функции .

Решение. Данная функция определена и непрерывна на , следовательно, вертикальных асимптот нет. Для определения наклонных асимптот находим пределы:

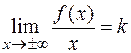и .

,

.

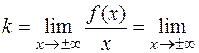
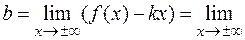
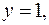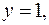Следовательно, у графика данной функции две односто­ронние горизонтальные асимптоты при –¥ и при –¥.

Пример. Найти асимптоты кривой .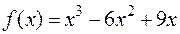

Решение. Данная функция определена и непрерывна на 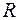, следовательно, вертикальных асимптот нет. Для определения наклонных асимптот находим пределы:

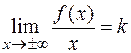и .

+¥.

Предел бесконечен, следова­тельно, кривая асимптот не имеет.

Общая схема исследования функции

Исследование дважды дифференцируемой функции на (за исключением, быть может, конечного множества точек) и построение ее графика можно выполнять по приводимой ниже схеме.

1. Установить область определения функции.

2. Если она симметрична относительно начала координат, проверить функцию на четность и нечетность.

3. Проверить функцию на периодичность.

4. Исследовать непрерывность функции. Определить поведение функции в окрестностях точек разрыва первого рода и граничных точек области определения. Для этого вычислить односторонние пределы функции при стремлении аргумента функции к указанным точкам.

5. Найди, если они существуют, асимптоты графика функций.

6. Определить интервалы возрастания и убывания функции, точки экстремума и экстремальные значения функции.

7. Найди интервалы выпуклости и вогнутости кривой и точки перегиба.

8. Определить, если это возможно, координаты точек пересечения графика функции с осями координат, а также нескольких дополнительных точек, принадлежащих графику.

Пример. Исследовать функцию 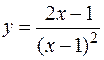и построить ее график.

Дата добавления: 2014-01-04