Первообразная функции и неопределённый интеграл

Несобственные интегралы

Определенные интегралы

Неопределенные интегралы

Первообразная функции и неопределённый интеграл ….……………..…4

Основные свойства неопределённого интеграла…….……………………6

Основные методы интегрирования ………………….…………………….8

Интегрирование рациональных дробей……………….…………………..11

Интегрирование тригонометрических выражений…...…………………..19

Интегрирование некоторых иррациональных функций…………………22

Интегральная сумма. Понятие определенного интеграла……….….…...26

Геометрический смысл определенного интеграла……………….……...27

Условия интегрируемости функций………………………………………28

Основные свойства определенного интеграла……………………………29

Определенный интеграл с переменным верхним пределом.…………… 33

Формула Ньютона-Лейбница.…………………………………………… 35

Основные методы вычисления определенного интеграла……………….36

Вычисление площадей плоских фигур в прямоугольной

системе координат………………………………………………..………. 38

Вычисление площадей плоских фигур в полярной

системе координат……………………..………………….……………….41

Несобственные интегралы с бесконечными пределами

интегрирования (первого рода).…………………………………………..44

Критерии сходимости несобственных интегралов второго рода.............47

Несобственные интегралы с бесконечными пределами

интегрирования (первого рода).…………………………………………..48

Критерии сходимости несобственных интегралов второго рода.............50

Литература…………………………………………………………………. 51

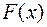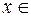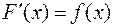Определение. Функция , называется пер­вообразной для функции на множестве X, если она дифференци­руема для любого Х и или .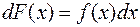

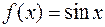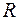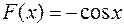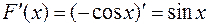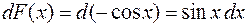Так, например, первообразной для функции на множестве является функция , так как или для.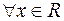

Теорема. Любая непрерывная на отрезке функция имеет на этом отрезке первообразную .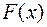

Будем рассматривать непрерывные на отрезке функции. Даже при таком ограничении задача восстановления функции 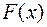по из­вестной производной (или известному дифференциалу) решается неоднозначно и не всегда просто.

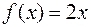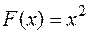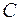Если, например, , то первообразной для этой функции является не только , но также и множество функций , где — произвольно выбранная постоянная.

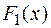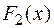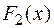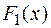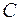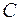Теорема. Если и — две различные первообразные одной и той же функции на множестве X то они отличаются друг от друга постоянным слагаемым, т. е. =+, где — постоянная.

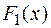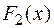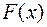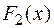
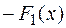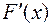
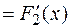
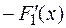
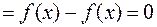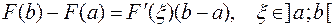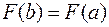
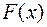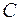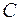Доказательство. Пусть и — первообразные функции на X. Их разность = является дифференцируемой функцией: . По теореме Лагранжа , но так как то следует, что = , где — постоянная, то есть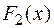 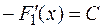или =+.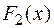

⊠

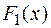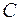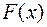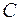Следствие. Если — некоторая первообразная функции на множестве X, то все первообразные этой функции определяются выражением , где — произвольная постоянная.

Операция отыскания первообразной 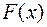функции называ­ется интегрированием.

Определение. Совокупность всех первообразных функции на множестве X называется неопределенным интегра­лом и обозначается

.

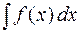В этой формуле 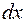называется подынтегральным выраже­нием, — подынтегральной функцией, 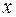— переменной интегриро­вания, а 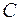— постоянной интегрирования.

Таким образом, неопределенный интеграл представляет собой любую функцию, дифференциал которой равен подынтегральному вы­ражению, а производная — подынтегральной функции.

Например:

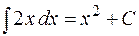, так как 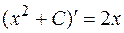или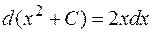

С геометрической точки зрения неопределенный интеграл пред­ставляет собой однопараметрическое семейство кривых 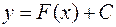(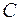— параметр).

На рисунке изображен неопределенный интеграл от функции 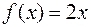, т. е. семейство парабол .

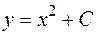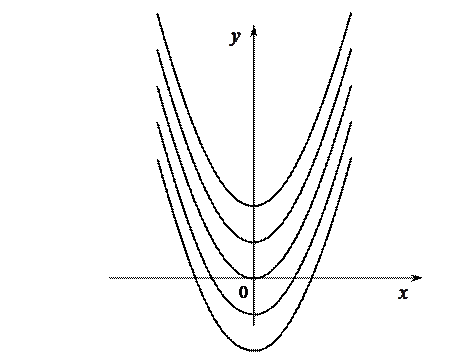
Кривые семейства [] называют интегральными кривыми. Они не пересека­ются между собой и не касаются друг друга. Через каждую точку плоскости про­ходит только одна интегральная кривая. Все интегральные кривые получаются одна из другой параллельным переносом вдоль оси .

Дата добавления: 2014-01-04