Основные методы интегрирования

Непосредственное интегрирование. Вычисление интегралов, осно­ванное на приведении подынтегрального выражения к табличной форме и использовании свойств неопределенного интеграла, называ­ется непосредственным интегрированием.

Пример. Найти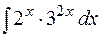

Решение. .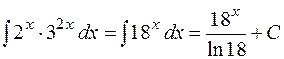

Интегрирование подстановкой (заменой переменной). Пусть тре­буется вычислить интеграл 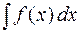, который не является таблич­ным.

Теорема. Пусть функция 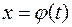определена и дифференци­руема на некотором множестве Т и пусть X — множество значений этой функции, на котором определена функция . Тогда, если на множестве X функция имеет первообразную, то на множестве Т справедлива формула

.

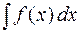
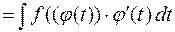Эта формула называется формулой замены переменной в не­определенном интеграле.

Суть метода подстановки состоит в том, что в интеграле 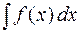переменную 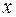заменяют переменной по формуле 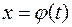, откуда .

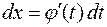В практике интегрирования чаще применяют подстановки в виде , то есть новая переменная интегрирования вводится как некоторая функция переменной .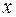

Пример. Найти .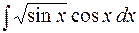

Решение. Сделаем подстановку:

Пример. Найти .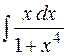

Решение. Сделаем подстановку:

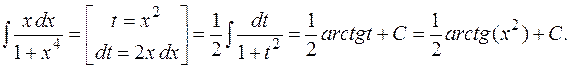
При интегрировании заменой переменной важно удачно сделать подстановку. Однако нельзя дать общее правило выбора замены переменной для интегрирования любой функции. Это можно сделать только для интегрирования отдельных классов функций (тригонометрических, иррациональных и т. д.).

Очень часто при вычислении интегралов пользуются приемом «подведения» подынтегральной функции под знак дифференциала. По определению дифференциала функции 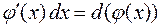. Переход от левой части этого равенства к правой называют «подведением» множителя 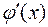под знак дифференциала, то есть

.

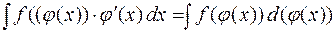Пример. Найти.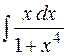

Решение.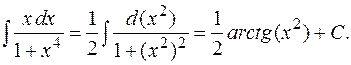

Пример. Найти .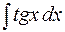

Решение.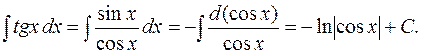

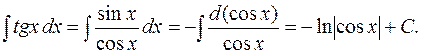
Заметим, что метод замены переменной основан на свойстве инвариантности формул интегрирования.

Интегрирование по частям. Метод интегрирования по частям следует из формулы дифференциала произведения двух функций. Пусть 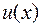и 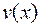— две дифференцируемые функции переменной 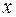.Тогда

.

Интегрируя обе части этого равенства, получаем

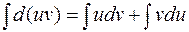, то так как 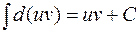, то

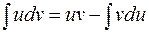. (1)

Соотношение (1) называется формулой интегрирования по частям. С помощью этой формулы отыскание интеграла 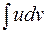можно свести к вычислению другого интеграла . Применять ее целесо­образно, когда интеграл в правой части формулы (1) более прост длявычисления, нежели исходный.

В формуле (1) отсутствует произвольная постоянная 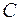, так как и в правой части этой формулы стоит неопределенный интеграл, со­держащий произвольную постоянную.

Пример. Найти .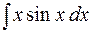

Решение.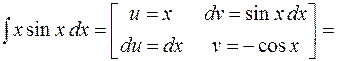

.

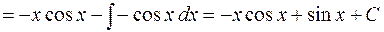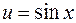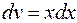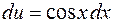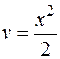Если в данном интеграле положить , , то , и

,

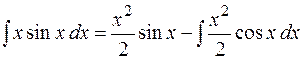т. е. в правой части получился более сложный интеграл, чем в левой. Значит, такое разбиение подынтегрального выражения на 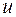и 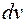является неудачным.

Дата добавления: 2014-01-04