Интегральная сумма. Понятие определенного интеграла

Определенный интеграл

Решение.

Выразим 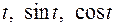через :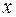

.

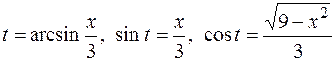Следовательно,

.

Пусть функция 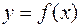определена и ограничена на отрезке , 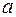<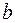. Разобьем произвольным образом на частичных отрезков точками 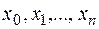и обозначим это разбиение через :

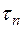Пусть 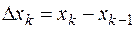— длина частичного отрезка , 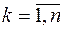. На каждом таком отрезке произвольным образом выбе­рем точку 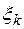и составим сумму:

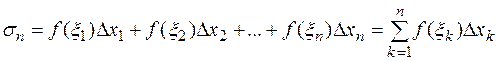(1)

Эта сумма называется интегральной суммой Римана для функции на отрезке , соответствующей данному разбиению 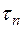отрезка и выбору промежуточных точек , .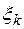

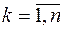Пусть — длина наибольшего частичного отрезка разбиения 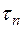: 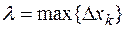, называемая диаметром разбиения.

Определение. Если существует конечный предел инте­гральной суммы (1) при 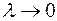, не зависящий от способа разбиения 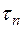отрезка на частичные отрезки и выбора промежуточных точек 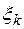, то этот предел называют определенным интегралом (или интегралом Римана) от функции на отрезке и обозначают

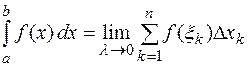(2)

Если указанный предел существует, то функция называется интегрируемой на отрезке (или интегрируемой по Риману). При этом 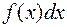называется подынтегральным выражением, — подынтегральной функцией, 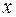— переменной интегрирования, 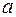и 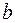— соответственно нижним и верхним пределами интегрирования.

Таким образом, определенный интеграл есть число, равное пределу, к которому стремится интегральная сумма, в случае, когда диаметр разбиения стремится к нулю.

Дата добавления: 2014-01-04