Понятие математической модели экономического процесса

СУЩНОСТЬ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ ЭКОНОМИЧЕСКИХ ПРОЦЕССОВ

Методические материалы по курсу лекций «Математическая экономика» для студентов специальности «Прикладная информатика в экономике»

1.	СУЩНОСТЬ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ ЭКОНОМИЧЕСКИХ ПРОЦЕССОВ
1.1	Понятие математической модели экономического процесса
1.2	Классификация математических моделей
1.3	Примеры построения математических моделей экономических задач
2.	ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
2.1	Постановка задачи линейного программирования
2.2	Линейное программирование в экономике
2.3	Графический метод решения задачи линейного программирования
2.4	Основная задача линейного программирования
2.5	Симплекс-метод
2.6	Пример расчета экономико-математической модели
2.7	Двойственная задача линейного программирования
2.8	Целочисленное линейное программирование
	ТРАНСПОРТНАЯ ЗАДАЧА
3.1	Построение транспортной модели
3.2	Сбалансированные и несбалансированные транспортные модели
3.3	Определение начального плана транспортировок.
3.4	Оптимальный план транспортной задачи. Метод потенциалов
3.5	Экономические задачи, сводящиеся к транспортным моделям
3.6	Венгерский метод решения задачи о назначениях
3.7	Примеры задачи о назначениях к решению экономических проблем
	НЕЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
4.1	Постановка задачи нелинейного программирования
4.2	Геометрическая интерпретация задачи нелинейного программирования
4.3	Метод множителей Лагранжа
4.4	Пример нелинейной экономико-математической модели
	ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
5.1	Постановка задачи динамического программирования.
5.2	Составление математической модели динамического программирования
5.3	Этапы решения задачи динамического программирования
5.4	Задача замены оборудования как задача динамического программирования
5.5.	Распределение инвестиций как задача динамического программирования
	МОДЕЛИ СИСТЕМ МАССОВОГО ОБСЛУЖИВАНИЯ (СМО)
6.1	Определение систем массового обслуживания (СМО)
6.2	Классификация СМО
6.3	Параметры СМО
6.4	Модели СМО с отказами.
6.5	Модели СМО с неограниченным временем ожидания
6.6.	Модели замкнутых СМО
	МОДЕЛИ СЕТЕВОГО ПЛАНИРОВАНИЯ И УПРАВЛЕНИЯ (СПУ)
	ЛИТЕРАТУРА

Из курса теории систем и системного анализа известно, что любая экономическая система состоит из управляемой части (объекта управления) и управляющей части (субъекта управления). Из этого же курса известно, что управление реальными экономическими системами носит многоуровневый характер, однако на каждом уровне управления можно выделить управляемую и управляющие части, а также внешнюю по отношению к рассматриваемой экономической системе среду. Принципиальная схема процесса управления некоторым экономическим объектом представлена на рисунке 1.1.

Рис.1.1 Общая схема процесса управления экономическим объектом

`Y(t) = <Y1(t),Y2(t),…,Ym(t)> -выходные переменные

`V(t) = <V1(t), V2(t),…, Vh(t)> -неуправляемые воздействия

Объект управления (управляемая часть) характеризуется набором переменных

`S(t) = <S1(t), S2(t),…, Sn(t)>, которые изменяются во времени под воздействием управляемых `X(t) = <X1(t), X2(t),…, Xk(t)> и неуправляемых `V(t)= <V1(t), V2(t),…, Vh(t)> воздействий. Неуправляемые воздействия представляют собой воздействие на экономическую систему со стороны внешней среды, а управляемые воздействия – это управляющие воздействия субъекта управления на объект управления.

Часть характеристик объекта управления при решении тех или иных проблем можно считать неизменными. Такие характеристики будем называть постоянными параметрами объекта управления и обозначать как `A = <A1, A2,…, Ak>.

Среди переменных, описывающих функционирование экономических объектов обычно выделяется группа переменных, по значениям которых оценивается качество функционирования. В экономических системах это может быть «прибыль», «рентабельность» «объем продаж» и т.п. Такие переменные будем называть выходными переменными (показателями эффективности) и обозначать как `Y(t) = <Y1(t), Y2(t),,…, Ym(t)>.

Очевидно, что задача субъекта управления – сформировать такие управляющие воздействия `X, чтобы добиться наилучших значений выходных переменных `Y.

Как правило, возможных вариантов (альтернатив) при выработке управляющих воздействий `X у субъекта управления несколько, в некоторых случаях количество возможных альтернатив (возможных значений `X) вообще стремится к бесконечности, поэтому у субъекта управления возникает проблема принятия оптимального решения. Проблема принятия решений была рассмотрена в курсе «Теория систем и системный анализ», поэтому здесь мы только коротко напомним о её сущности.

Процесс принятия решения состоит в определении:

Цели – что нужно достигнуть в результате решения задачи (при формировании цели субъект управления ориентируется на свои собственные предпочтения, на задания вышестоящего уровня управления и т.п.);

Средств – какими ресурсами мы можем воспользоваться для достижения цели;

Критерия (критериев) – требования к достижению цели. Критерий (критерии) позволяют выбрать лучшее решение.

Возможных путей (альтернатив) достижения цели.

Для принятия решения нужно получить выражение, связывающее цель со средствами. Такие выражения в различных прикладных областях получили названия: критерий функционирования, критерий или показатель эффективности, целевая или критериальная функция, функция цели и т.п.

Если удается построить такое выражение, каким бы сложным оно не было, то задача почти всегда может быть решена, то есть формализованное представление задачи позволяет потом использовать формализованные методы анализа проблемной ситуации.

Следует отметить, что среди критериев могут быть и принципиально неформализуемые (красота, комфорт, безопасность). В этих случаях полностью формализованная постановка задачи оказывается нереализуемой, и для принятия решений следует использовать интуицию и опыт экспертов

В курсе экономической математике будут рассматриваться случаи, когда могут быть использованы формализованные методы анализа и решения проблем, то есть такие случаи, когда между выходными переменными `Y и остальными характеристиками экономической системы может быть установлена зависимость, описываемая с помощью математических соотношений.

Изменения переменных `S (t), описывающих состояние объекта управления и изменения выходных переменных `Y(t) происходят под воздействием управляемых `X(t) и неуправляемых (возмущающих) `V(t) воздействий:

`X[t,t+Dt], `V[t,t+Dt] - соответственно управляющие и возмущающие воздействия на объект управления на отрезке времени [t, t+Dt].

Выражения для Q и F могут иметь самый разнообразный вид, но если их можно представить в виде определенных математических зависимостей, то тогда выражения (1) представляют собой математическое описание (математическую модель) процесса функционирования исследуемой экономической системы (процесса).

Задача субъекта управления – сформировать такие управляющие воздействия `X, чтобы добиться наилучших значений выходных переменных `Y.

Очевидно, что «наилучшие» значение выходных переменных следует трактовать в смысле выбранного критерия эффективности W(t) = W(Y1(t), Y2(t),,…, Ym(t))

Самый простой случай, когда критерий эффективностиW состоит из одного элемента, то есть качество функционирования объекта управления описывается одной переменной: W(t) = Y, а целью управления является максимизация (либо минимизация) значений этой выходной переменной. Соотношение (1) при этом трансформируются в соотношение:

Однако, даже в этом случае, далеко не всегда связь между выходной переменной «Y» и остальными характеристиками системы очевидна, и зависимость «F» представляет собой достаточно простое математическое выражение.

Простейший случай, когда Y зависит только от вектора управляемых переменных `X и постоянных параметров `A. В практике управления экономическими объектами такого рода задачи могут возникать на заданном временном интервале, когда изменениями состояния объекта управления можно пренебречь, а неуправляемые воздействия либо не учитывать, либо заменять их некоторыми усредненными значениями, которые рассматриваются как дополнительные постоянные параметры.

В итоге математическая модель процесса управления экономическим объектом принимает вид:

j – система ограничений, вытекающая из физической и (или) экономической сущности решаемой задачи управления. Сама задача состоит в нахождении таких значений управляемых переменных `X, которые при соблюдении системы ограничений j обеспечат максимальное (либо минимальное, в зависимости от условий решаемой задачи) значение показателя эффективности Y.

Рассмотрим простейший пример, иллюстрирующий сказанное выше.

Из листа бумаги заданного размера (a – ширина листа, b – длина листа) необходимо изготовить коробочку (без крышки) в форме правильного параллелепипеда максимального объема.

При решении любой проблемы формализованными методами, как следует из представленной на рис. 1.1 принципиальной схемы управления, необходимо, прежде всего, определиться с составляющими решаемой задачи:

- какие переменные `S характеризуют состояние объекта управления?;

- какими постоянными параметрами `A характеризуется объект управления?;

- воздействуют ли на объект и какие неуправляемые воздействия `V?;

- на что может воздействовать субъект управления, то есть, каким является набор управляемых переменных `X, значения которых субъект управления может выбирать по своему усмотрению?;

- что является целью решаемой задачи, какие выходные переменные `Y являются существенными с точки зрения достижения цели решаемой задачи, каков критерий эффективности достижения цели?

- какие ограничения, следующие из физической или экономической сущности задачи, накладываются на значения управляемых переменных?

Только после ответов на эти вопросы можно приступать к построению математической модели, описывающей функционирование рассматриваемой системы (процесса, задачи управления).

В нашем случае объект управления (лист бумаги) описывается только постоянными параметрами- линейными размерами листа, то есть множество переменных характеристик `S является пустым, а множество постоянных характеристик `A состоит из двух элементов: a и b (a – ширина листа, b – длина листа), то есть `S = Ø; ` A = <a,b>.

На исследуемый объект не воздействует никаких внешних факторов, поэтому множество неуправляемых воздействий `V является пустым: `V = Ø.

Очевидно, что при построении коробочки есть всего одна управляемая переменная – это высота коробочки. Действительно, для построения коробочки следует задаться ее высотой и, сделав соответствующие разрезы по краям листа (см. рис.1.2), согнуть и склеить коробочку. Таким образом, множество управляемых переменных `X состоит из одного элемента: `X = < x >, где x – высота коробочки.

Поскольку целью решения является построение коробочки максимального объема, то выходной переменной, существенной с точки зрения достижения цели, является объем построенной коробочки, то есть множество существенных выходных переменных `Y состоит из одной переменной: `Y = Y, где Y – объем коробочки. Соответственно и критерий эффективности W состоит из одного элемента: W = Y = F (x,a,b) и заключается в максимизации значения Y.

Определив состав исходных параметров и переменных, можно приступить к построению математической модели задачи. В данном случае это несложно сделать даже ученику шестого класса. Очевидно, что объем коробочки (Y) связан с управляемой переменной (x) и постоянными параметрами (a и b) следующим соотношением: Y = (a-2x) (b-2x)x.

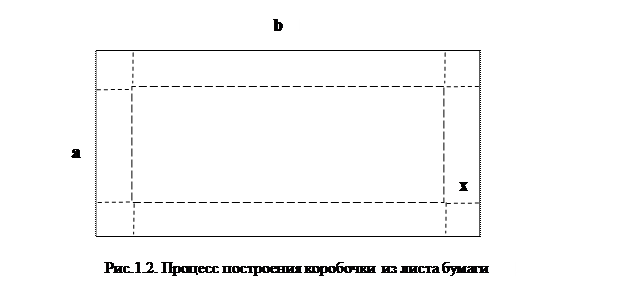
Исходя из размеров листа, можно сформулировать и ограничения на значения управляемой переменной x: значение x должно быть положительным, но при этом быть меньшим, чем ½ ширины листа (предполагается, что ширина листа меньше его длины), то есть: 0 < x < a/2.

В итоге получим математическую модель процесса построения коробочки в виде:

Построение математической модели – это только первый этап экономико-математического моделирования. На втором этапе происходит использование построенной модели для решения тех или иных задач управления, анализа, исследования экономических систем. Чаще всего с помощью построенной математической модели пытаются найти оптимальное управленческое решение – оптимальные значений управляемых переменных, которые при соблюдении системы ограничений, накладываемых на функционирование объекта управления, обеспечат наилучшие значения выходных переменных в соответствии с выбранным критерием эффективности. В нашем простейшем примере необходимо найти такое значение переменной x (высоты коробочки), которое обеспечит её максимальный объем.

В зависимости от вида полученной на первом этапе математической модели может быть два подхода к ее использованию для получения оптимального (или близкого к нему) управленческого решения. Первый используется тогда, когда может быть получено «аналитическое решение», то есть с помощью определенных аналитических процедур найдено точное оптимальное решение. В нашем случае функция Y= F(x)= (a-2x) (b-2x)x является непрерывной дифференцируемой функцией управляемой переменной x. Из курса высшей математики известно, что необходимое условие экстремума функции одной переменной – это равенство нулю её первой производной, то есть Y’_x=0. Выполнив дифференцирование, получим: -2(b-2x)x -2(a-2x)x+(a-2x)(b-2x)=0. После раскрытия скобок и упрощения получим квадратное уранение следующего вида: 12x²– 4(a + b)x +ab =0. Корни данного уравнения, как известно из курса алгебры за 6 класс средней школы, находятся по известной формуле:

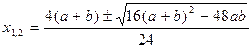
Используя ограничения на x (x > 0; x < a/2), можно получить единственное решение, которое и будет оптимальным управленческим решением, определяющим высоту коробочки.

Однако, даже если такую задачу предложить решить ученикам, например, 9-ого класса, которые ещё не знают дифференциального исчисления и правила нахождения экстремума функций одной переменной, решение задачи может быть получено следующим образом. Вся область допустимых значений x: (0, a/2) разбивается на m отрезков (например, равной длины): [0,a/2m], [a/2m, 2a/2m], [2a/2m, 3a/2m],…, [(m-1)a/2m,a/2]. Для каждой из точек a/2m, 2a/2m, 3a/2m,…, (m-1)a/2m по формуле (3) находим значение Y.

В качестве решения задачи (высоты коробочки) выберем ту точку (из a/2m, 2a/2m, 3a/2m,,…, (m-1)a/2m), в которой достигается максимальное значение Y. Таким образом, построенную математическую модель экономического процесса (задачи) можно использовать для нахождения близких к оптимальному значению управленческих решений и не зная аналитических методов решения модели, путем перебора значений управляемых переменных из области допустимых решений, которая определяется системой ограничений

В курсе экономической математики будет рассмотрен ряд математических моделей экономических процессов (модели линейного программирования, модели динамического программирования, модели систем массового обслуживания и др.) и изучены методы аналитического решения этих моделей. Тем не менее, основное в экономико-математическом моделировании – это умение строить математические модели, то есть основным является первый этап – этап построения математической модели исследуемого экономического процесса (задачи). Забегая несколько вперед, отметим, что представленная выше форма математической модели (2) называется моделью математического программирования. Аналитические решения получены только для некоторых частных случаев функций f и j. Например, если функции f и j линейны относительно управляемых переменных `X, то задача является задачей линейного программирования, для которой разработаны эффективные методы решения. Если функция f является непрерывной, дифференцированной, а ограничения j заданы в форме равенств, то задача может быть решены с помощью множителей Лагранжа и т.д.

В случае необходимости учета динамики объекта управления, то есть когда управляющие решения нужно принимать на достаточно длительном временном интервале, разбитом на более короткие временные отрезки, на каждом из которых в зависимости от текущего состояния объекта управления принимаются управленческие решения, можно использовать методы динамического программирования, которые также будут изучены в курсе «Экономическая математика».

Часто в практике управления экономическими объектами возникают задачи, когда сама связь между различными характеристиками системы не ясна. Например, очевидно, что снижение цены на некоторый производимой фирмой товар (цена – управляемая переменная, входящая в состав вектора управления `X) приводит к увеличению спроса на данный товар (спрос – неуправляемое воздействие среды на объект, входящее в состав вектора неуправляемых воздействий `V). Однако, вид зависимости между ценой и спросом не описывается очевидной формулой. Эта зависимость проявляется в вероятностном смысле. Изучение такого рода зависимостей опирается на наличие статистических данных за прошедшие периоды функционирования системы и производится с помощью эконометрических моделей, которые были изучены в курсе «Эконометрика». В этом же курсе изучались модели зависимости выходных переменных (элементов вектора `Y) от времени (анализ временных рядов), которые используются в том случае, когда на выходные переменные действуют самые разнообразные неуправляемые воздействия, и установить причинно-следственные связи между ними не представляется возможным. Кроме эконометрических моделей, которые уже изучены Вами, есть еще ряд типичных моделей, в которых существенную роль играют статистические факторы. Это, в частности, модели систем массового обслуживания. Модели таких систем будут изучены в курсе «Экономическая математика». Кроме перечисленных моделей при изучении курса Вы познакомитесь также с примерами графических и игровых моделей, используемых для анализа и управления экономическими системами.

Еще раз остановимся на первом и основном этапе – этапе построения математической модели исследуемого экономического процесса (задачи). В середине прошлого века, когда математические модели стали практически использоваться при принятии управленческих решений, процесс построения математической модели получил название «операционное исследование», а методология построения математических моделей экономических процессов выделилась в специальную науку, получившую название «исследование операций».

Впервые математические модели были использованы для решения практической задачи в 30-х годах в Великобритании при создании системы противовоздушной обороны. Для разработки данной системы были привлечены ученые различных специальностей. Система создавалась в условиях неопределенности относительно возможных действий противника, поэтому исследования проводились на адекватных математических моделях. В это время впервые был применен термин: «операционное исследование», подразумевавший исследования военной операции. В последующие годы операционные исследования или исследования операций развиваются как наука, результаты которой применяются для выбора оптимальных решений при управлении реальными процессами и системами.

Можно выделить следующие основные этапы операционного исследования:

- наблюдение явления и сбор исходных данных;

- тестирование модели и анализ выходных данных. Если полученные результаты не удовлетворяют исследователя, то следует либо вернуться
на этап 3, т.е. предложить для решения задачи другую математическую модель; либо вернуться на этап 2, т.е. поставить задачу более корректно;

Таким образом, операционное исследование является итерационным процессом, каждый следующий шаг которого приближает исследователя к решению стоящей перед ним проблемы. В центре операционного исследования находятся построение и расчет математической модели.

Определение 1.1.1. Математическая модель – это система математических соотношений, приближенно, в абстрактной форме описывающих изучаемый процесс или систему.

Определение 1.1.2. Экономико-математическая модель – это математическая модель, предназначенная для исследования экономической проблемы.

Применение математических моделей необходимо в тех случаях, когда проблема сложна, зависит от большого числа факторов, по-разному влияющих на ее решение. В этом случае непродуманное и научно не обоснованное решение может привести к серьезным последствиям. Примеров этому в нашей жизни имеется немало, в частности в экономике. Использование математических моделей позволяет осуществить предварительный выбор оптимальных или близких к ним вариантов решений по определенным критериям. Они научно обоснованы, и лицо, принимающее решения, может руководствоваться ими при выборе окончательного решения. Следует понимать, что не существует решений, оптимальных «вообще». Любое решение, полученное при расчете математической модели, оптимально по одному или нескольким критериям, предложенным постановщиком задачи и исследователем. Кстати, практика показывает, что заниматься операционными исследованиями и построением математических моделей лучше всего не «чистым» математикам, не всегда представляющим себе сущность изучаемой проблемы и уделяющим большее внимание различным математическим тонкостям построения и расчета, и не предметникам, которые не всегда могут корректно поставить задачу. Хорошие результаты получают специалисты, знающие предметную область и вместе с тем владеющие математическими методами исследования. Поэтому данное учебное пособие может быть рекомендовано не только студентам экономических специальностей, но и всем тем, кто интересуется применением математических моделей в экономике.

В настоящее время математические модели применяются для анализа, прогнозирования и выбора оптимальных решений в различных областях экономики. Это планирование и оперативное управление производством, управление трудовыми ресурсами, управление запасами, распределение ресурсов, планировка и размещение объектов, руководство проектом, распределение инвестиций и т.п.