Примеры построения математических моделей экономических задач

Классификация математических моделей

Авторами предлагается классификация математических моделей, представленная на рис.1.3.

По числу критериев эффективности математические модели делятся на однокритериальные и многокритериальные. Многокритериальные математические модели содержат два и более критерия.

По учету неизвестных факторов математические модели делятся на детерминированные, стохастические и модели с элементами неопределенности.

В стохастических моделях неизвестные факторы – это случайные величины, для которых известны функции распределения и различные статистические характеристики (математическое ожидание, дисперсия, среднеквадратическое отклонение и т. п.). Среди стохастических можно выделить:

- модели стохастического программирования, в которых либо в целевую функцию (1.2.1), либо в ограничения (1.2.2) входят случайные величины;

- модели теории случайных процессов, предназначенные для изучения процессов, состояние которых в каждый момент времени является случайной величиной;

- модели теории массового обслуживания, в которой изучаются многоканальные системы, занятые обслуживанием требований. Также к стохастическим моделям можно отнести модели теории полезности, поиска и принятия решений.

Для моделирования ситуаций, зависящих от факторов, для которых невозможно собрать статистические данные и значения которых не определены, используются модели с элементами неопределенности. В моделях теории игр задача представляется в виде игры, в которой участвуют несколько игроков, преследующих разные цели, например организацию предприятия в условиях конкуренции.

В имитационных моделях реальный процесс разворачивается в машинном времени, и прослеживаются результаты случайных воздействий на него, например организация производственного процесса.

Данное учебное пособие посвящено изучению, прежде всего детерминированных моделей, а также знакомит студентов с примерами стохастических моделей.

В детерминированных моделях неизвестные факторы не учитываются. Несмотря на кажущуюся простоту этих моделей, к ним сводятся многие практические задачи, в том числе большинство экономических задач. По виду це-

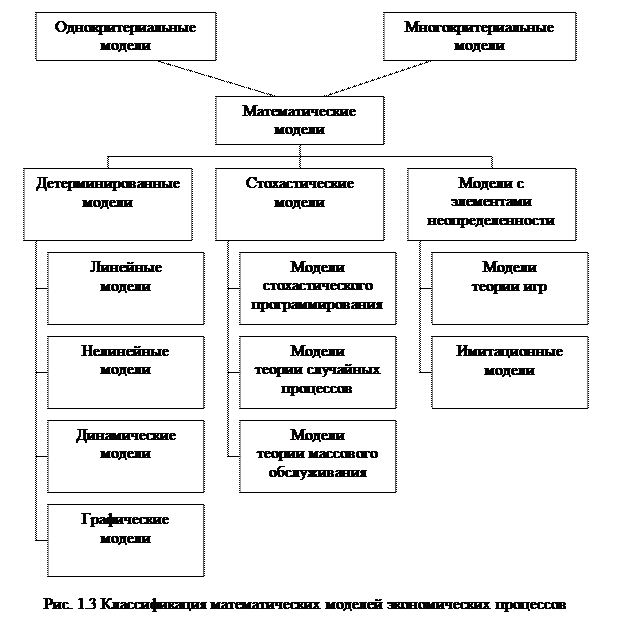
левой функции и ограничений детерминированные модели делятся на линейные, нелинейные, динамические и графические.

В линейных моделях целевая функция и ограничения линейны по управляющим переменным. Построение и расчет линейных моделей являются наиболее развитым разделом математического моделирования, поэтому часто к ним стараются свести и другие задачи либо на этапе постановки, либо в процессе решения.

Для линейных моделей любого вида и достаточно большой размерности известны стандартные методы решения, часть из которых будет освещена в данном пособии.

Нелинейные модели – это модели, в которых либо целевая функция, либо какое-нибудь из ограничений (либо все ограничения) нелинейны по управляющим переменным. Для нелинейных моделей нет единого метода расчета. В зависимости от вида нелинейности, свойств функции и ограничений можно предложить различные способы решения. Однако может случиться и так, что для поставленной нелинейной задачи вообще не существует метода расчета. В этом случае задачу следует упростить, либо сведя ее к известным линейным моделям, либо просто линеаризовав модель.

В динамических моделях в отличие от статических линейных и нелинейных моделей учитывается фактор времени. Критерий оптимальности в динамических моделях может быть самого общего вида (и даже вообще не быть функцией), однако для него должны выполняться определенные свойства. Расчет динамических моделей сложен, и для каждой конкретной задачи необходимо разрабатывать специальный алгоритм решения.

Графические модели используются тогда, когда задачу удобно представить в виде графической структуры.

Рассмотрим следующую задачу.

Предприятие располагает определенными производственными мощностями для изготовления изделий и может выпускать изделия фиксированных наименований для их последующей реализации. Требуется определить оптимальный состав производственного заказа и способы его изготовления.

Построение математической модели.

1. Цель:

- максимизация прибыли от реализации;

- минимизация себестоимости изготовления;

- минимизация времени обработки.

Выходные переменные модели `Y: прибыль от реализации (Y1),

себестоимость изготовления (Y2), время обработки (Y3).

2. Параметры модели (постоянные параметры `A):

- – число единиц оборудования;

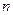- – число наименований изделий, которое может выпускать предприятие;

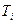- – фонд времени работы i-й единицы оборудования ;

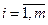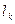- – число различных способов изготовления изделия 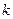-гo наименования, характеризующихся различным временем обработки на единице оборудования -го типа ;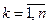

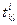- – время обработки изделия 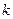-го наименования, изготавливаемого 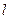-м способом на оборудовании -го типа ;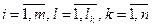

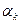- – спрос на изделие 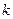-го наименования;

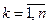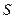- – размер склада, предусмотренного для хранения изделий, выраженный в количествах изделий;

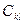- – себестоимость изготовления изделия 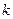-го наименования 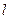-м способом ;

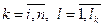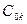- – требуемая себестоимость изготовления изделия 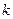-го наименования ;

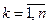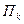- – прибыль от реализации изделия 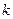-го наименования ;

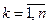3. Управляющие переменные `X:

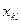– число изделий 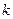-го наименования, выпускаемых l -м способом ;

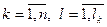4. Определение области допустимых решений (системы ограничений φ):

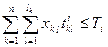, (1.3.1)

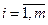– ограничение по фонду работы оборудования;

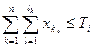– ограничение по размеру склада; (1.3.2)

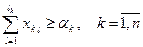– ограничение по спросу; (1.3.3)

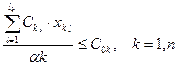– ограничение по себестоимости изготовления; (1.3.4.)

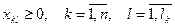1.3.5.)

5. Выражение критерия эффективности через параметры и управляющие переменные модели.

1) Максимизация прибыли.

Y1 - суммарная прибыль.

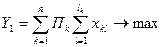(1.3.6)

2) Минимизация себестоимости.

Является критерием при отсутствии ограничения (1.3.4).

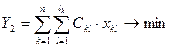(1.3.7)

3) Минимизация суммарного времени обработки Y3, выраженного, например, в станко-часах.

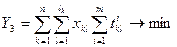(1.3.8)

Таким образом, построены три однокритериальные линейные модели:

(1.3.1) – (1.3.6) – формирование производственного заказа по критерию максимизации прибыли;

(1.3.1) – (1.3.3), (1.3.5), (1.3.7) – организация производственного процесса по критерию минимальной себестоимости изготовления;

(1.3.1) – (1.3.5), (1.3.8) - организация производственного процесса по критерию минимального времени изготовления.

Если прибыль нелинейно зависит от числа выпускаемых изде­лий,

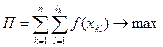, (1.3.10)

где 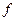– некоторая нелинейная функция, то переходим к нелинейной оптимизационной модели (1.3.1) – (1.3.5), (1.3.10).

Модель (1.3.1) – (1.3.5), (1.3.6), (1.3.8) является многокритериальной.

Решениями исходной задачи, получаемыми в результате расчета любой из предложенных моделей, служат значения переменных 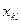; ; 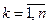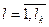, которые удовлетворяют ограничениям, сформулированным в пункте 4, и доставляют экстремум одному или нескольким выбранным критериям оптимизации.

После изучения раздела 1 следует выполнить контрольную работу № 1.

Дата добавления: 2014-01-04