Целочисленное линейное программирование. Метод Гомори

Двойственная задача линейного программирования. Экономическая интерпретация

Рассмотрим задачу линейного программирования следующего вида:

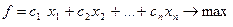(2.7.1)

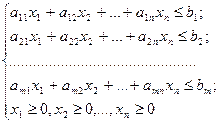(2.7.2)

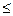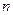В задаче требуется максимизировать целевую функцию; все ограничения являются неравенствами со знаком , все переменные неотрицательны. Задача содержит управляющих переменных и ограничений. Коэффициенты при переменных в целевой функции: 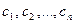; свободные члены: .

Двойственная задача линейного программирования имеет вид

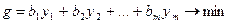(2.7.3)

(2.7.4)

В двойственной задаче требуется найти минимум целевой функции, ограничения – неравенства со знаком 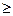, управляющие переменные 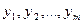неотрицательны. Задача содержит управляющих переменных и 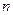ограничений. Коэффициенты целевой функции задачи являются свободными членами исходной ЗЛП, а свободные члены двойственной задачи 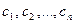– коэффициентами целевой функции исходной ЗЛП. Матрица коэффициентов двойственной задачи транспонирована, т.е. строки заменены столбцами, а столбцы – строками.

Задачи (2.7.1), (2.7.2) и (2.7.3), (2.7.4) называются парой взаимно двойственных задач линейного программирования.

Для двойственных задач верна следующая теорема.

Теорема двойственности: если одна из взаимно двойственных задач имеет оптимальное решение х*, то другая также имеет оптимальное решение у*. При этом соответствующие им оптимальные значения целевых функций и равны.

Поясним экономический смысл двойственной модели.

Пусть в качестве управляющих переменных 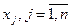исходной модели рассматривается число изделий, производимых некоторым предприятием, а параметрами – количество ресурсов -го типа, используемых для изготовления изделий. Через обозначено количество ресурсов -го типа, идущее на изготовление одного изделия 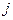-го вида, (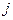– прибыль от реализации одного изделия 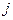-го вида). Тогда исходная модель (2.7.1), (2.7.2) соответствует задаче определения оптимального плана производства продукции, обеспечивающего максимальную прибыль.

Пусть предприятие решило прекратить производство изделий и продать ресурсы, идущие на их изготовление. Обозначим через 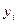цены на единицу ресурсов -го вида, 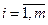. Цены на ресурсы должны удовлетворять следующим двум условиям: во-первых, они не должны быть слишком высокими, иначе ресурсы невозможно будет продать; а во-вторых, цены на ресурсы должны быть такими, чтобы прибыль от их реализации была больше прибыли от реализации готовой продукции. Первое условие выражается формулой (2.7.3), второе условие – ограничениями (2.7.4). В левой части каждого из неравенств (2.7.4) стоит прибыль от продажи ресурсов всех типов, идущих на изготовление 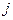-го изделия, в правой части – прибыль от продажи 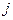-го изделия, 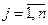. Таким образом, двойственная задача (2.7.3) – (2.7.4) соответствует следующей экономической проблеме: по каким минимальным ценам следует продавать ресурсы, чтобы прибыль от их реализации была больше прибыли, полученной от реализации продукции, изготавливаемой с использованием этих ресурсов. Значения переменных 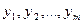часто называют теневыми ценами.

Построение двойственной задачи позволяет глубже разобраться в поставленной экономической проблеме.

Если управляющие переменные в задаче линейного программирования определяют количество единиц неделимой продукции, то оптимальное решение должно быть получено в целых числах. К задачам такого типа относится большое число экономических задач, например распределение производственных заказов между предприятиями, оптимальный раскрой материалов, определение загрузки оборудования, распределение транспортных средств по рейсам, задачи производства и реализации неделимой продукции. Если единица составляет малую часть от общего количества, например при планировании массового и крупносерийного производства, то для нахождения оптимального решения применяют обычный симплекс-метод и округляют полученное решение до целого. В противном случае, например при планировании производства или реализации автомобилей, округление может привести к решению, далекому от оптимального. Линейные задачи, решение которых должно быть получено в целых числах, называют задачами целочисленного программирования (ЦЛП).

Математическая модель, задачи ЦЛП имеет следующий вид:

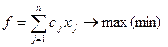(2.8.1)

(2.8.2)

где Z — множество целых чисел.

Для решения задачи ЦЛП может быть применен метод Гомори.

Метод Гомори содержит два этапа.

Этап 1. Решение исходной задачи обычным симплекс-методом и проверка решения на целочисленность. Если решение содержит хотя бы одно дробное значение, то переходят к этапу 2, в противном случае расчет заканчивается.

Этап 2. Составление дополнительного ограничения (сечения) и решение расширенной задачи обычным симплекс-методом. Дополнительное ограничение (сечение) отсекает нецелочисленные решения.

Сечение обладает следующими двумя свойствами:

1) любое целочисленное решение ему удовлетворяет;

2) любое нецелочисленное решение задачи ему не удовлетворяет.

Объясним, как составляется сечение.

Пусть выполнен этап 1;

;

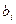– дробное число. Рассмотрим -е ограничение:

Так как 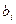– дробное, а в правой части все переменные целые, то хотя бы одно, значение должно быть дробным.

Возьмем дробную часть от левой и правой частей ограничения.

Обозначим через {r} дробную часть числа r.

Дробная часть суммы не превосходит суммы дробных частей слагаемых, поэтому

Дробная часть произведения не превосходит произведения целого на дробную часть, следовательно:

В результате имеем

Обозначим

,

.

Тогда из последнего неравенства получаем

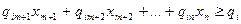
Отняв от левой части неравенства дополнительную неотрицательную переменную, переходим к уравнению

,

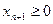
При дополнении этого ограничения к исходной задаче мы получили задачу большей размерности.

Эту задачу решают обычным симплекс-методом, т.е. переходят к этапу 1.

Если при решении задачи симплекс-методом имеется несколько дробных решений, то дополнительные ограничения следует составлять для значения, имеющего максимальную дробную часть.

Дата добавления: 2014-01-04