Пример расчета экономико-математической модели

Предприятие рекламирует свою продукцию с использованием четырех источников массовой информации: телевидения, радио, газет и расклейки объявлений. Анализ рекламной деятельности в прошлом показал, что эти средства приводят к увеличению прибыли соответственно на 10, 5, 7 и 4 усл. ед., в расчете на 1 усл. ед., затраченную на рекламу. На рекламу выделено 50000 усл. ед. Администрация предприятия не намерена тратить на телевидение более 40%, а на радио и газеты – более 50% от общей суммы выделенных средств. Как следует предприятию организовать рекламу, чтобы получить максимальную прибыль?

Решение.

Составим математическую модель задачи.

Цель – максимизация прибыли.

Параметрами являются все числа, приведенные в условии задачи.

Управляющие переменные:

– количество средств, вложенных в рекламу на телевидение;

– количество средств, вложенных в рекламу на радио;

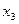– количество средств, вложенных в рекламу в газетах;

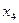– количество средств, вложенных в рекламу, организованную с помощью расклейки объявлений.

Область допустимых решений имеет, вид

(2.6.1)

Она содержит ограничения по общей сумме выделенных средств, по количеству средств, предусмотренных на рекламу по телевидению, на радио и в газетах, и условия неотрицательности управляющих переменных.

Критерий оптимальности записывается следующим образом:

(2.6.2)

(2.6.1), (2.6.2) – математическая модель задачи организации рекламной деятельности.

Целевая функция и ограничения линейны по управляющим переменным, следовательно, это задача линейного программирования.

Приведем задачу к каноническому виду, добавив дополнительные переменные к левым частям ограничений (2.6.1). Получим

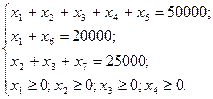(2.6.3)

Задача (2.6.1), (2.6.3) может быть решена симплекс-методом. Решение.

Шаг 1. Получение начального решения.

Базисные переменные: , , .

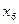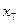Свободные переменные: , , , .

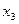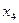Начальное решение:

.

Шаг 2. Функция 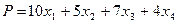уже выражена через свободные переменные.

Шаг 3. Проверка решения на оптимальность. Составляем симплекс-таблицу (табл. 2.6.1).

Таблица 2.6.1

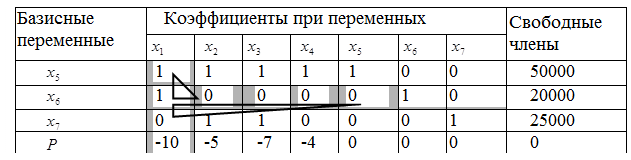
Решение неоптимально, так как последняя строка содержит отрицательные числа.

Шаг 4. Получение нового решения.

Максимальное по абсолютной величине отрицательное число последней строки – это -10; следовательно, первый столбец является разрешающим и переменная вводится в список базисных переменных. Найдем переменную, выводимую из списка базисных переменных. Для этого подсчитаем отношения элементов столбца свободных членов к элементам разрешающего столбца и выберем среди них минимальное

Вторая строка является разрешающей, и переменная 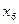должна быть выведена из списка базисных переменных.

Разрешающий элемент .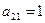

Составим новую симплекс-таблицу.

Для подсчета элементов новой симплекс-таблицы по формулам (2.5.4, 2.5.5) удобно использовать правило треугольника, наглядно отображающее указанные формулы.

Правило треугольника. Для получения элемента новой симплекс-таблицы надо от элемента предыдущей симплекс-таблицы, стоящего на том же месте, отнять следующее выражение: произведение элемента разрешающей строки, стоящего в одном столбце с данным элементом, на элемент данной строки, стоящий в одном столбце с разрешающим элементом, деленное на разрешающий элемент. Это выражение как бы соответствует треугольнику.

В качестве примера в табл. 2.6.1 нарисованы треугольники, использующиеся для расчета и .

Таким образом, все элементы разрешающей строки делятся на разрешающий элемент. Остальные элементы пересчитываются по правилу треугольника.

Новая симплекс-таблица имеет следующий вид (табл. 2.6.2):

Таблица 2.6.2

Базисные переменные	Коэффициенты при переменных	Свободные члены
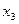
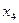
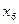
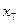
						-1
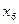
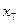
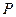
		-5	-7	-4

Новое решение имеет вид

Таким образом, прибыль увеличилась на 200000 усл. ед.

Это решение неоптимально, так как последняя строка содержит отрицательные числа.

Продолжаем оптимизацию.

Разрешающий столбец – третий, так как ему соответствует максимальное по абсолютной величине отрицательное число -7.

Следовательно, третья строка является разрешающей.

Разрешающий элемент: =1.

Перейдем к новой симплекс-таблице (табл. 2.6.3).

Таблица 2.6.3

Базисные переменные	Коэффициенты при переменных	Свободные члены
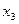
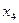
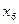
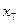
						-1	-1
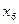
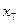
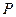
				-4

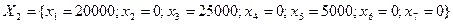
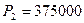
Прибыль выросла, но решение 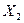неоптимально, так как в последней строке еще осталось отрицательное число.

Получим новое решение.

Разрешающий столбец – четвертый, следовательно, переменная 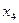вводится в список базисных переменных.

Разрешающая строка – первая, и переменная выводится из списка базисных переменных.

Новая симплекс-таблица имеет следующий вид (табл. 2.6.4):

Таблица 2.6.4

Базисные переменные	Коэффициенты при переменных	Свободные члены
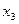
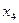
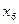
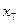
						-1	-1
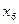
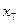
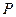
						-6

Последнее решение является оптимальным, поскольку все числа, стоящие в последней строке, неотрицательны. Это решение единственно, так как все элементы последней строки, соответствующие свободным переменным , , , 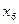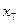строго положительны.

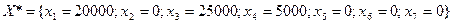
Таким образом, для получения максимальной прибыли в размере 395000 усл. ед. надо распределить средства следующим образом: 20000 усл. ед. вложить в рекламу на телевидении; 20000 усл. ед. вложить в рекламу в газетах и 5000 усл. ед. вложить в рекламу, организованную с помощью расклейки объявлений. Рекламу на радио организовывать не следует.

Изложенные выше вычисления проводились для случая, когда начальное решение является допустимым. Если в начальном решении существуют , то допустимое начальное решение можно найти по следующему алгоритму.

Шаг 1. Выражение функции 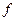через свободные переменные.

Шаг 2. Составление симплекс-таблицы.

Шаг 3. Выбор переменной, вводимой в список базисных переменных.

Просматривается строка, содержащая максимальный по абсолютной величине отрицательный свободный член, и по максимальному по абсолютной величине отрицательному элементу этой строки выбирается разрешающий столбец, например столбец с номером 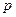. Переменная, стоящая в этом столбце, вводится в список базисных переменных. Если просматриваемая строка не содержит отрицательных элементов, то система ограничений несовместна, исходная задача решений не имеет.

Шаг 4. Выбор переменной, выводимой из списка базисных переменных.

Находят отношения элементов столбца свободных членов к элементам разрешающего столбца. Рассматривают отношения, в которых числитель и знаменатель отрицательные, и среди них выбирают минимальное. Строка, соответствующая выбранному отношению, например 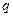-я, является разрешающей, и переменная, стоящая в этой строке, выводится из списка базисных переменных. Элемент 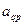, стоящий на пересечении разрешающей строки и разрешающего столбца, является разрешающим элементом.

Шаг 5. По формулам (2.5.4) и (2.5.5) проводят симплекс-преобразование и переходят к новой симплекс-таблице. Если в новой таблице все свободные члены неотрицательны, то найденное решение является допустимым и следует перейти к шагу 3 алгоритма симплекс-метода, в противном случае – к шагу 2 рассматриваемого алгоритма.

Заметим, что существуют различные программы, реализующие симплекс-метод на персональном компьютере. Исследователю нужно только построить линейную модель и ввести исходные данные. Все расчеты, изложенные выше, на персональном компьютере осуществятся в течение нескольких секунд.

После изучения данного раздела целесообразно решить задачу 2 контрольной работы № 3.

Дата добавления: 2014-01-04