Пример 4.2.1

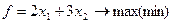
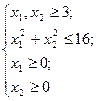
В соответствии с алгоритмом построим на плоскости 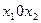область допустимых решений (рис. 4.2.1)

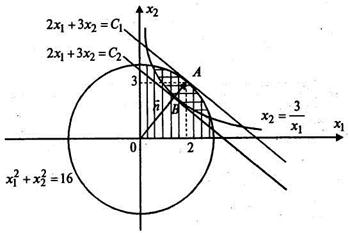
Рис. 4.2.1

Ограничения 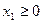, 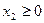выделяют на плоскости 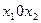первую четверть.

Границей полуплоскости, соответствующей первому ограничению,

является гипербола

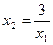
Неравенство выполняется для точек, лежащих выше гиперболы.

Границей полуплоскости, определяемой вторым ограничением, является окружность с центром в точке (0,0) и радиусом, равным 4. Искомая полуплоскость заштрихована вертикальной штриховкой. Область допустимых решений выделена горизонтальной штриховкой.

Функция возрастает в направлении вектора-нормали 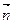с координатами (2,3), и ее линии уровня расположены перпендикулярно вектору-нормали 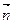. Таким образом, максимум достигается в точке А, а минимум – в точке В.

Заметим, что в точке А совпадают тангенсы углов наклона касательной к окружности 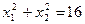и прямо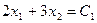й к оси 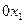. Тангенсы углов наклона касательной и прямой к оси 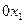определяются значениями производных по соответствующих функций. Для прямой 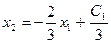тангенс равен .

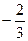Продифференцируем выражение 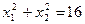как неявную функцию от . Получаем

,

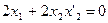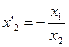
Приравниваем значения тангенсов, получаем

,

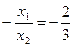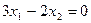
К этому уравнению добавим уравнение окружности, которой принадлежит точка А.

Получаем систему

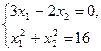
Решив ее, найдем оптимальное решение

; ;

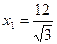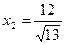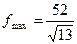
Аналогично определим координату точки В, в которой тангенс угла наклона к оси 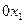прямой 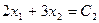совпадает с тангенсом угла наклона касательной к функции .

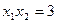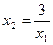
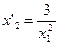
Получаем уравнение

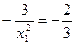
Вторым для нахождения координат точки является уравнение гиперболы, которой принадлежит точка В:

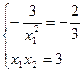
Из последней системы найдем оптимальное решение, соответствующее минимальному значению ,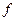

, ,

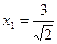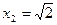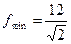
Дата добавления: 2014-01-04