Метод множителей Лагранжа

Пусть требуется решить задачу нелинейного программирования следующего вида:

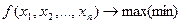(4.3.1)

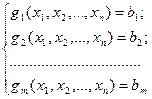(4.3.2)

где функци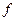и и 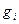, непрерывны, и непрерывны их част­ные производные по , .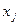

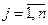Для решения поставленной задачи может быть применен метод множителей Лагранжа. Объясним идею метода на примере ЗНП, зависящей от двух переменных.

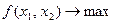
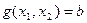
На плоскости 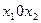уравнение 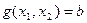определяет график некоторой функции, представленный на рис. 4.3.1. На нем показаны несколько линий уровня некоторой функции 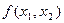и выбранное в качестве примера направление ее возрастания.

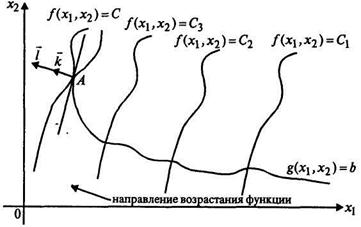
Рис. 4.3.1

В точке А, в которой функция 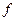достигает максимального значения, совпадают касательные линии к графикам функци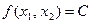й

и .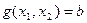

Следовательно, в точке А векторы-нормали к функциям 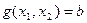и 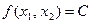пропорциональны. Обозначим эти векторы соответственно через 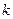и 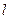. Получаем

,

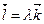где 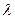– некоторый коэффициент пропорциональности. Координатами векторов 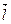и 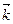являются значения частных производных функци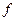й и 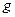соответственно в точке А.

;

.

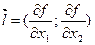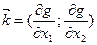Из условия пропорциональности в точке А имеем

;

.

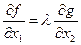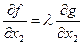Для определения значений 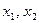, в которых функция 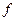достигает максимума, к этим уравнениям надо добавить условие принадлежности точки А графику функции .

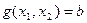Окончательно получаем систему уравнений, определяющую оптимальное решение поставленной задачи

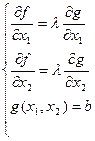
Введем новую функцию

.

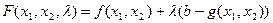Тогда последняя система перепишется в виде

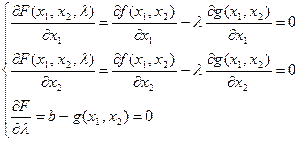
Функцию 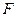называют функцией Лагранжа.

Дата добавления: 2014-01-04