
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Пример 5.4.1
|
|
|
|
Задача замены оборудования как задача динамического программирования
В общем виде проблема ставится следующим образом: определить оптимальную стратегию использования оборудования в период времени длительностью  лет, причем прибыль за каждые
лет, причем прибыль за каждые  лет,
лет, 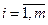 от использования оборудования возраста
от использования оборудования возраста 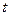 лет должна быть максимальной.
лет должна быть максимальной.
Известны:  – выручка от реализации продукции, произведенной за год на оборудовании возраста
– выручка от реализации продукции, произведенной за год на оборудовании возраста 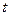 лет,
лет,  – годовые затраты, зависящие от возраста оборудования
– годовые затраты, зависящие от возраста оборудования 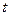 ,
, 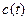 – остаточная стоимость оборудования возраста
– остаточная стоимость оборудования возраста 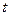 лет,
лет, 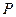 – стоимость нового оборудования. Под возрастом оборудования понимается период эксплуатации оборудования после последней замены, выраженный в годах.
– стоимость нового оборудования. Под возрастом оборудования понимается период эксплуатации оборудования после последней замены, выраженный в годах.
Для построения математической модели последовательно выполняются этапы, сформулированные ниже.
1. Определение числа шагов. Число шагов равно числу лет, в течение которых эксплуатируется оборудование.
2. Определение состояний системы. Состояние системы характеризуется возрастом оборудования 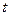 ;
; 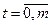 .
.
3. Определение управлений. В начале  -го шага,
-го шага, 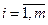 может быть
может быть
выбрано одно из двух управлений: заменять или не заменять
оборудование. Каждому варианту управления приписывается
число
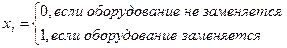 (5.4.1)
(5.4.1)
4. Определение функции выигрыша на  -м шаге. Функция выигрыша на
-м шаге. Функция выигрыша на  -м шаге – это прибыль от использования оборудования к концу
-м шаге – это прибыль от использования оборудования к концу  -го года эксплуатации,
-го года эксплуатации, 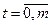 ,
, 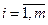 .
.
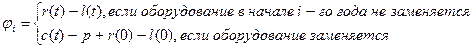 (5.4.2)
(5.4.2)
Таким образом, если оборудование не продается, то прибыль от его использования – это разность между стоимостью произведенной продукции и эксплуатационными издержками. При замене оборудования прибыль составляет разность между остаточной стоимостью оборудования и стоимостью нового оборудования, к которой прибавляется разность между стоимостью продукции и эксплуатационными издержками для нового оборудования, возраст которого в начале  -го шага составляет 0 лет.
-го шага составляет 0 лет.
5. Определение функции изменения состояния.
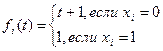 (5.4.3)
(5.4.3)
6. Составление функционального уравнения для i=m.
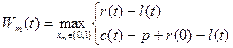 (5.4.4)
(5.4.4)
7. Составление основного функционального уравнения
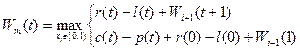 (6.4.5)
(6.4.5)
где 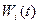 — прибыль от использования оборудования возраста t лет с
— прибыль от использования оборудования возраста t лет с  -го шага (с конца
-го шага (с конца  -го года) до конца периода эксплуатации.
-го года) до конца периода эксплуатации.
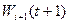 — прибыль от использования оборудования возраст а
— прибыль от использования оборудования возраст а 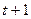 год с (
год с (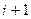 )-го шага до конца периода эксплуатации;
)-го шага до конца периода эксплуатации;
Таким образом, математическая модель задачи построена.
Расчет модели проведем для конкретного примера.
 =12,
=12, 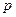 =10,
=10, 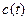 =0,
=0, 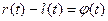
Значения 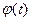 заданы в табл. 5.4.1
заданы в табл. 5.4.1
Таблица 5.4.1

Для данного примера функциональные уравнения будут иметь вид
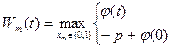 ;
;

Для решения данной задачи заполняется табл. 5.4.2.
Таблица 5.4.2
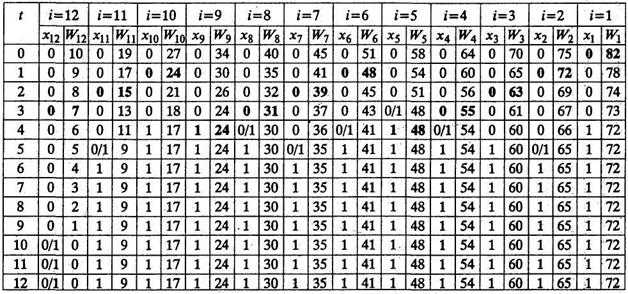
В левой колонке таблицы записываются возможные состояния системы 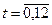 , в верхней строке – номера шагов
, в верхней строке – номера шагов 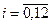 . Для каждого шага определяются условные оптимальные управления
. Для каждого шага определяются условные оптимальные управления 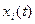 и условный оптимальный выигрыш
и условный оптимальный выигрыш 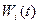 с
с  -го шага и до конца для оборудования возраста
-го шага и до конца для оборудования возраста 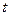 лет.
лет.
Поясним, как заполняется таблица для нескольких шагов.
1. Условная оптимизация начинается с последнего 12-го шага. Для  =12 рассматриваются возможные состояния системы
=12 рассматриваются возможные состояния системы 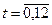 . Функциональное уравнение на 12-м шаге имеет вид
. Функциональное уравнение на 12-м шаге имеет вид
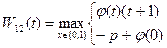
1)t=0
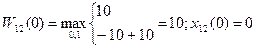
2)t=1
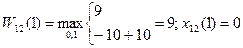
………………..
10)t=9
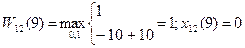
11)t=10
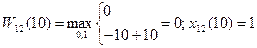
…………………
13)t=13
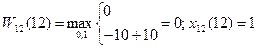
Таким образом, на 12-м шаге оборудование возраста 0 — 9 лет заменять не надо. Оборудование возраста 10—12 лет можно заменить или продолжить его эксплуатацию, так как для t=10, 11, 12 имеется два условных оптимальных управления 1 и 0.
По результатам расчетов заполняются два столбца таблицы, соответствующие  =12.
=12.
2. Условная оптимизация 11-го шага.
Для  =11 рассматриваются все возможные состояния системы t= 0,1,2,...,12.Функциональное уравнение на 11-м шаге имеет вид
=11 рассматриваются все возможные состояния системы t= 0,1,2,...,12.Функциональное уравнение на 11-м шаге имеет вид
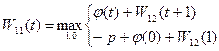
 =11
=11
1)t=0

2)t=2
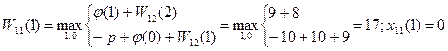
……………………………
6)t=5
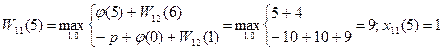
7)t=6
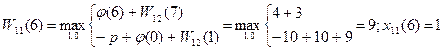
…………………………..
13)t=12
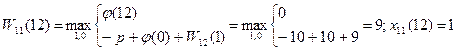
Таким образом, на 11-м шаге не следует заменять оборудование возраста 0—4 года. Для оборудования возраста 5 лет возможны две стратегии использования: заменить или продолжать эксплуатировать.
Начиная с 6-го года оборудование следует заменять. По результатам расчетов заполняются два столбца таблицы, соответствующие  =11,
=11,  =10
=10
1)t=0
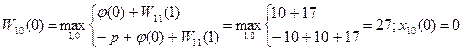
2)t=1
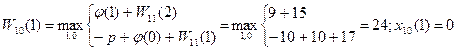
3)t=2
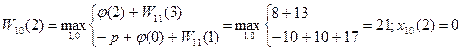
4)t=3
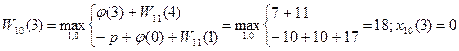
5)t=4
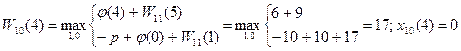
……………………………
13)t=12
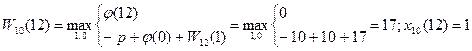
На 10-м шаге не следует заменять оборудование возраста 0-3 года. Начиная с 4-го года оборудование следует заменять, так как новое оборудование приносит большую прибыль.
По результатам расчетов заполняются два столбца, соответствующие  =10.
=10.
Аналогичным образом заполняются остальные девять столбцов таблицы. При расчетах 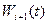 на каждом шаге значения
на каждом шаге значения 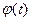 для каждого
для каждого 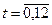 берутся из таблицы исходных данных, приведенной в уcловии задачи, а значения
берутся из таблицы исходных данных, приведенной в уcловии задачи, а значения 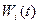 – из последнего, заполненного на предыдущем шаге столбца.
– из последнего, заполненного на предыдущем шаге столбца.
Этап условной оптимизации заканчивается после заполнения табл. 5.4.2.
Безусловная оптимизация начинается с первого шага.
Предположим, что на первом шаге  =1 имеется новое оборудование, возраст которого 0 лет.
=1 имеется новое оборудование, возраст которого 0 лет.
Для 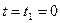 оптимальный выигрыш составляет
оптимальный выигрыш составляет 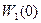 =82. Это значение соответствует максимальной прибыли от использования нового оборудования в течение 12 лет.
=82. Это значение соответствует максимальной прибыли от использования нового оборудования в течение 12 лет.
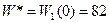
Выигрышу 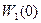 =82 соответствует безусловное оптимальное управление
=82 соответствует безусловное оптимальное управление 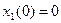 .
.
Для  =2 по формуле (5.4.3)
=2 по формуле (5.4.3) 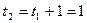 .
.
Безусловное оптимальное управление 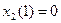 .
.
Для  =3
=3 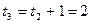 .
.
Безусловное оптимальное управление 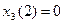 .
.
И далее соответственно
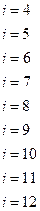
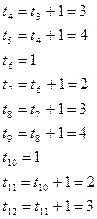
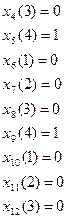
Управления, составляющие оптимальную стратегию использования оборудования, выделены в табл. 5.4.2 жирным шрифтом.
В рамках данной задачи оптимальная стратегия заключается в замене оборудования при достижении им возраста 4-х лет. Аналогичным образом можно определить оптимальную стратегию использования оборудования любого возраста. Предлагаем читателю самостоятельно в этом убедиться.
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 366; Нарушение авторских прав?; Мы поможем в написании вашей работы!