Пример 5.5.1

Оптимальное распределение инвестиций как задача динамического программирования

Инвестор выделяет средства в размере 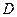условных единиц, которые должны быть распределены между -предприятиями. Каждое -е предприятие при инвестировании в него средств 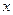приносит прибыль 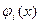усл. ед., 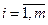. Нужно выбрать оптимальное распределение инвестиций между предприятиями, обеспечивающее максимальную прибыль.

Выигрышем W данной задаче является прибыль, приносимая -предприятиями.

Построение математической модели.

1. Определение числа шагов. Число шагов т равно числу предприятий, в которые осуществляется инвестирование.

2. Определение состояний системы. Состояние системы на каждом шаге характеризуется количеством средств 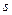, имеющихся в наличии перед данным шагом, .

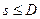3. Выбор шаговых управлений. Управлением на -м шаге 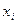, 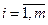является количество средств, инвестируемых в -е предприятие.

4. Функция выигрыша на -м шаге

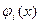(5.5.1)

— это прибыль, которую приносит -е предприятие при инвестировании в него средств .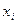

,

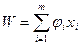следовательно, данная задача может быть решена методом динамического программирования.

5. Определение функции перехода в новое состояние.

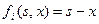(5.5.2)

Таким образом, если на -м шаге система находилась в состоянии s, а выбрано управление х, то на 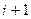-м шаге система будет находиться в состоянии 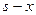. Другими словами, если в наличии имеются средства в размере s усл. ед., и в -е предприятие инвестируется х усл. ед., то для дальнейшего инвестирования остается 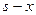усл. ед.

6. Составление функционального уравнения для i=m.

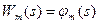, (5.5.3)

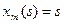(5.5.4)

На последнем шаге, т.е. перед инвестированием средств в последнее предприятие, условное оптимальное управление соответствует количеству средств, имеющихся в наличии; т.е. сколько средств осталось, столько и надо вложить в последнее предприятие. Условный оптимальный выигрыш равен доходу, приносимому последним предприятием.

7. Составление основного функционального уравнения. Подставив в формулу (5.2.4) выражения (5.5.1) и (5.5.2), получаем следующее функциональное уравнение

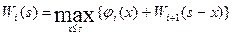(5.5.5)

Поясним данное уравнение. Пусть перед -м шагом у инвестора остались средства в размере s ycл. ед. Тогда х усл. ед. он может вложить в -e предприятие, при этом оно принесет доход 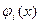, а оставшиеся 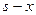усл. ед.– в остальные предприятия с 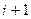-го до т- го. Условный оптимальный выигрыш от такого вложения 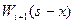. Оптимальным будет то условное управление х, при котором сумма 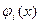и 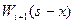максимальна.

Проведем численный расчет модели.

D =5000, m =3.

Значение 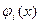, 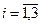заданы в табл. 5.5.1

Таблица 5.5.1

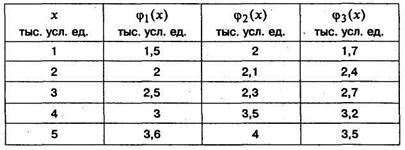
Для , ,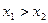

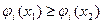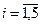
Для простоты в задаче сделано предположение, что вкладываются только тысячи условных единиц.

Проведем условную оптимизацию. По ее результатам заполняется табл. 5.5.2.

Таблица 5.5.2

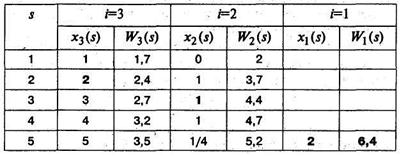
В первой колонке таблицы записываются возможные состояния системы 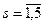, в верхней строке – номера шагов 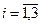. На каждом шаге определяются условные оптимальные управления 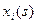и условные оптимальные выигрыши , , .

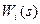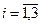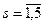1. Проведение условной оптимизации для последнего шага =3. Функциональное уравнение на последнем шаге имеет вид

, ,

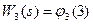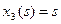поэтому два столбца табл. 6.5.2, соответствующие =3, заполняются автоматически по таблице исходных данных.

2. Условная оптимизация для =2.

Функциональное уравнение

.

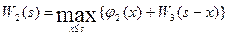Для проведения условной оптимизации заполним ряд вспомогательных таблиц (табл. 5.5.3–5.5.8), соответствующих различным значениям s, т.е. различным исходам окончания предыдущего шага.

1) s =l

Таблица 5.5. 3

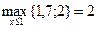, следовательно

2) s =2

Таблица 5.5.4

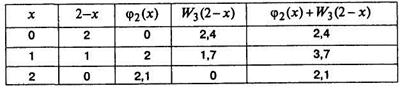
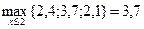, следовательно

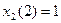
3) s =3

Таблица 5.5.5

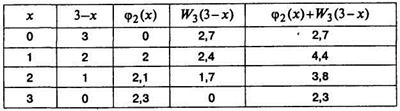
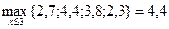
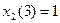
4) s =4

Таблица 5.5.6

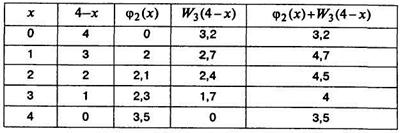
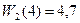
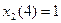
5) s =5

Таблица 5.5.7

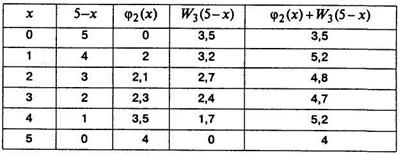
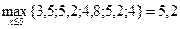
Для s =5 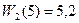возможны два условных оптимальных управления

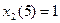и

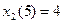
3. Условная оптимизация для =l.

Перед первым шагом состояние системы известно.

s = D =5 тыс. усл. ед., и условную оптимизацию следует проводить только для этого значения

s =5

Таблица 5.5.8

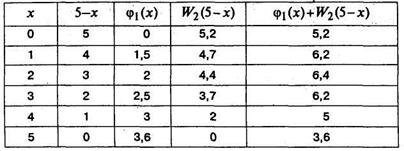
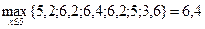, следовательно,

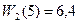
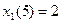
Оптимальная прибыль, приносимая тремя предприятиями при инвестировании в них 5 тыс. усл. ед., равна 6,4 тыс. усл. ед.

Проведем безусловную оптимизацию.

Ее результаты отмечены в таблице.

; .

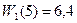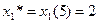Для 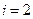по формуле (6.5.2) .

; .

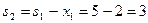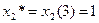Для .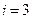

; .

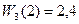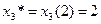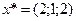
Таким образом, для получения максимальной прибыли в размере 6400 усл. ед. следует по 2000 усл. ед. вложить в первое и третье предприятия и 1000 усл. ед. – во второе предприятие.

Следует понимать, что полученное решение есть лишь некоторое приближение к оптимальному решению. Его можно улучшить, т.е. приблизить к оптимальному, взяв более мелкий шаг оптимизации, например вкладывать в предприятия средства, кратные 500 усл. ед. В заключение следует отметить, что после построения математической модели динамического программирования, т.е. выполнения этапов 1–7 пункта 6.2, для расчета модели может быть составлена программа. Использование компьютера позволит решить задачу большой размерности, т.е. получить решение, достаточно близкое к оптимальному.

После изучения данного раздела следует выполнить контрольную работу № 5

Дата добавления: 2014-01-04