Кинематика материальной точки

Г.Ростов- на – Дону

Учебное пособие

Монастырский Л.М.

ОСНОВЫ МЕХАНИКИ ДЛЯ СТУДЕНТОВ

РАСШИРЕННОГО НАПРАВЛЕНИЯ «ФИЗИКА»

для студентов физических специальностей университетов

В настоящее время издано огромное количество учебников по курсу «Общая физика» для студентов высших учебных заведений, обучающихся по специальностям «естественнонаучное образование» и «физико-математическое образование». Однако при чтении лекций пользоваться только каким-либо одним из них не представляется возможным ни для преподавателя, ни для студента. Более того, роль лектора не сводится к пересказыванию содержания учебника, даже самого удачного, целиком. Всегда необходимо отбирать материал, соответствующий рабочей программе данной специальности и пристрастиям лектора.

В данном конспекте лекций по разделу курса общей физики «Механика» сделана попытка изложить соответствующий материал логически замкнуто и методически обосновано. Особое внимание при этом уделяется понятиям модели в физике, способам выбора модели и их теоретическому описанию. Много внимания моделям уделяется при введении понятия взаимодействия и обоснованию необходимости раздельного появления силы трения покоя и силы трения скольжения.

Тщательно рассматриваются границы применимости тех или иных физических законов, а также релятивистское и нерелятивистское приближение в механике.

В основу физики как учебного предмета положена физика как наука, что позволяет опираться на основные законы механики и показывать, как они работают в разных условиях.

Достаточно много внимания уделяется графическим иллюстрациям к теоретическому материалу, которые является неотъемлемой частью лекции. Это позволяет включать пространственное воображение слушателя и делает более наглядными сложные математические выкладки.

Следует заметить, что поскольку физика наука, возникшая из эксперимента, лекции следует сопровождать показом демонстраций, логически связанных с теоретическим материалом. В конспекте лекций приведены ссылки на возможные варианты демонстрационного эксперимента, что очень удобно для лектора. Кроме того, приведены примеры некоторых задач, которые также можно приводить для демонстрации возможных применений тех или иных физических законов.

ОСНОВЫ КЛАССИЧЕСКОЙ МЕХАНИКИ

Физика – наука об окружающем нас мире. Физика – наука опытная. Ее цель и задачи состоят в том, чтобы понять всю природу, как разные проявления одной совокупности физических явлений и происходящих в ней процессов. Открыть законы, стоящие за этими процессами и объединить отдельные явления природы, предварительно разъединив их для подробного изучения.

Физика, как наука, возникла благодаря, прежде всего, трудам греческого философа Аристотеля (384 – 322 г.г. до н.э.). Аристотель собрал и систематизировал огромный естественнонаучный материал предшественников (как говорят, он владел всеми знаниями той эпохи) и сам осуществил ряд глубоких наблюдений. Несмотря на то, что в его взглядах на строение окружающего нас мира было много заблуждений, они просуществовали около 16 веков, т.к. во многом совпадали с догматами церкви. Следующий шаг в развитии физики и, прежде всего механики, сделали итальянский ученый Галилео Галилей (1564 – 1642 г.г.) и англичанин Исаак Ньютон (1643 – 1727 г.г.). Именно они заложили основы так называемой классической механики, которую мы будем изучать в течение всего первого семестра.

1. Движение в пространстве. Способы задания положения тел в пространстве (векторный способ, координатный способ, «естественный» способ).

Механика – раздел физики, в котором изучается механическое движение, т.е. изменение положения тел в пространстве относительно других с течением времени. Механика, в свою очередь, чисто формально, разделяется на кинематику и динамику. В кинематике изучается механическое движение без выяснения причины того или иного характера движения (состояние покоя, равномерного прямолинейного движения или движение с ускорением).

Как ни странно, механика не может точно описать ни один реальный физический процесс, происходящий в окружающем нас мире. Дело в том, в ходе каждого реального процесса происходит множество тесно связанных друг с другом явлений, которые не поддаются математическому описанию (составлению формул). Выход состоит в том, чтобы пользоваться моделями, поддающимися математическому описанию. От модели совсем не требуют внешнего сходства с описываемым объектом, достаточно, чтобы совпадали их свойства. Такой моделью в механике является материальная точка.

Материальная точка это тело, размерами которого можно пренебречь в условиях данной задачи. Например, в одних задачах Землю можно считать материальной точкой, а в других – нельзя.

Основными физическими понятиями раздела «Кинематика материальной точки» являются: механическое движение, траектория, система отсчета, путь и перемещение, средняя и мгновенная скорость, равномерное прямолинейное движение, ускорение.

Механическое движение – изменение положения тел в пространстве относительно других тел. Рассмотрим для начала способы задания положения тел в пространстве (идет речь о материальных точках).

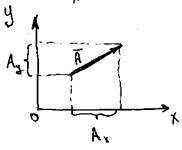
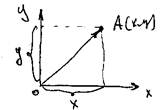
Обратимся к рис.1(а,б).

а) б)

Рис.1

На рис.1 (а) показаны декартовы координаты х, у точки А на плоскости. Здесь же приведен радиус-вектор этой точки А. Видно, что координаты радиус-вектора точки А совпадают с ее декартовыми координатами. На рис. 1 (б) приведены проекции на оси координат произвольного вектора (проведенного не из начала координат).

Любой вектор удобно представлять с помощью единичного вектора некоторого произвольного направления. На рис.2 представлено некоторое произвольное направление и указан единичный вектор этого направления .

Рис.2

Тогда любой вектор этого направления можем записать в следующем виде:

.

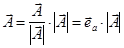Радиус – вектор удобно разлагать по осям координат с помощью единичных векторов- ортов. Рассмотрим рис.3.

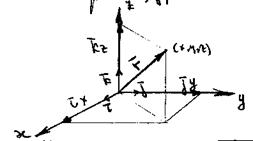
Рис.3

Здесь 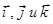- единичные векторы (орты) декартовой системы координат в пространстве. Тогда разложение радиус-вектора 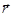по ортам выглядит следующим образом:

.

Рассмотрим теперь способы задания положения точки в пространстве.

1. Векторный способ.

В этом способе следует задать начало отсчета – точку О. Тогда положение некоторой точки А относительно этого начала отсчета можно задать с помощью радиус-вектора, как показано на рис.4. Таким образом, задается зависимость .

Рис.4

Геометрическое место точек концов радиус-вектора называется траекторией. Введем вектор перемещения, как . Назовем средней скоростью движения величину:

.

Видно, что направление средней скорости совпадает с направлением вектора перемещения.

Если уменьшать интервал времени 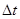, то в пределе получим мгновенную скорость следующим образом:

.

Мгновенная скорость представляет собой производную по времени от радиус-вектора.

Замечание.

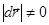Отметим, что в общем случае . Например, в случае движения точки по окружности с постоянной по модулю скоростью ясно, что, и, следовательно, d0. С другой стороны, , т.к. вектор все время изменяет свое направление.

При изменении скорости возникает ускорение, которое можно определить следующим образом: 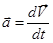, или с помощью разложения по ортам декартовой системы координат:

.

Таким образом, зная зависимость , можно вычислить скорость и ускорение тела в любой момент времени.

Существует и обратная задача – зная ускорение в виде зависимости , найти скорость и перемещение тела. Для решения этой задачи воспользуемся интегральным исчислением. По определению 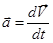и правую часть этого выражения можно рассматривать, как производную скорости по времени, с другой стороны, ее можно рассматривать как отношение двух бесконечно малых величин – дифференциала (бесконечно малого приращения) скорости dV и дифференциала (бесконечно малого приращения) времени dt. Тогда следует очевидное:

.

Отсюда можно записать при V₀ =0:

.

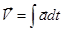Найдем теперь перемещение тела, используя определение мгновенной скорости:

.

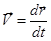Тогда можем записать , или окончательно .

Поскольку для модуля мгновенной скорости можем записать 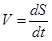, где S – путь, пройденный телом вдоль траектории, то величину этого пути можно найти с помощью следующего выражения:

.

2. Координатный способ.

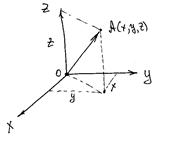Задавим начало отсчета точку О, и свяжем с ней декартову систему координат в пространстве (рис. 5).

Рис. 5

Тогда, зная зависимости координат частицы от времени, можно рассчитать ее скорость и ускорение в любой другой момент времени следующим образом:

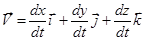и

и .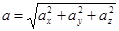

Также это дает возможность рассчитать направление векторов скорости и ускорения по формулам:

, , .

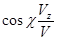3. «Естественный» способ.

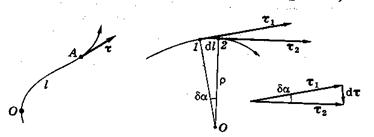Это способ задания положения точки в пространстве с помощью параметров траектории. Рассмотрим рис.6.

Рис. 6

Точка О задает начало отсчета для движения вдоль траектории точки А. Измеряя длину траектории l от начала О до положения точки в данный момент времени, можно задавать положение точки в любой момент времени.

Введем единичный вектор касательной к траектории в данной точке . При движении вдоль траектории произвольной формы меняется направление этого вектора , следовательно, он изменяется во времени.

Поскольку, по определению, мгновенная скорость является производной перемещения по времени, а вектор перемещения совпадает с хордой, соединяющей два последовательных положения тела А и В, то направление вектора скорости в данной точке совпадает с предельным положение хорды, т.е. с касательной (см. рис. 7).

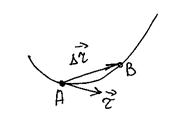Рис. 7

Можем теперь написать 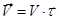. Здесь V- модуль вектора скорости. Более точной является запись .

Найдем мгновенное ускорение точки по формуле:

.

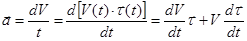Чисто формально (с точки зрения математики) ускорение разделилось на две составляющие его части. Попытаемся найти физический смысл каждой составляющей. Первое слагаемое назовем тангенциальным, поскольку его направление совпадает с направлением касательной к траектории движения точки. Выясним более подробно смысл величины 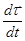, являющейся производной единичного вектора касательной по времени.

Производная единичного вектора по времени.

По определению производной 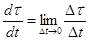. С другой стороны, , вектор

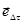представляет собой направление вектора . Теоретически доказывается, вектор

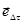направлен перпендикулярно касательной к траектории в данной точке, а 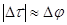(угол поворота вектора ). Следовательно, можем написать:

.

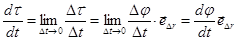По определению при вращательном движении по окружности угловая скорость 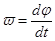, следовательно:

.

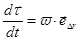Поскольку существует связь модуля угловой и линейной скорости (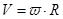), то можем записать:

.

Теперь для полного ускорения можем записать следующую формулу:

.

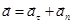Здесь - тангенциальное ускорение, направленное по касательной к траектории в данной точке. Оно определяет изменение модуля скорости.

Другая составляющая полного ускорения , где - единичный вектор нормали к касательной в данной точке траектории (см. рис. 8).

Рис. 8

Полное ускорение теперь записывается в виде:

= + .

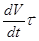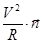Дата добавления: 2014-01-04