Закон всемирного тяготения

Как уже отмечалось, гравитационное взаимодействие очевидно одно из самых универсальных в природе, ему подчинены все материальные тела. Этому взаимодействию соответствует сила гравитационного взаимодействия, которая удовлетворяет закону всемирного тяготения Ньютона.

Закон всемирного тяготения в следующем виде справедлив для материальных точек массами m₁ и m₂, находящимися на расстоянии r друг от друга:

.

В таком виде закон всемирного тяготения справедлив еще для тел, имеющих форму шара, если под r понимать расстояние между их центрами.

Однако это только выражения для модуля этой силы. Векторная величина силы всемирного тяготения определяется следующим выражением (см. рис.16):

.

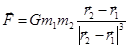Рис. 16

Гравитационная постоянная G была измерена Г. Кавендишем в 1798 г. с помощью крутильных весов, изображенных на рис. 17.

Рис. 17.

Сила взаимодействия больших и малых шаров измерялась по величине угла закручивания нити подвеса весов.

Сила тяжести.

На все тела вблизи поверхности Земли действует сила взаимодействия, которую, называют силой тяжести. Величина силы тяжести равна F=mg. Она только приблизительно равна силе гравитационного взаимодействия тела и Земли, вследствие движения Земли вокруг собственной оси вращения.

Вес тела.

Вес тела это сила, с которой тело давит на опору или растягивает нить подвеса. Вес тела численно равен силе нормального давления тела на опору. Он зависит от состояния опоры (а именно, от характера ее движения). Если же тело не давит на опору и не растягивает подвес, то тело находится в состоянии невесомости. Для невесомости характерно действие на тело только одной силы – силы тяжести.

В выражение входит масса, которая ранее была определена, как мера инертности тела. В этот же закон входит так называемая гравитационная масса. Но инертность и способность к гравитационному взаимодействию представляют собой физически разные свойства. Если инертная масса определяется в динамическом эксперименте, то гравитационная масса определяется в статическом эксперименте взвешиванием. Можем записать в гравитационном поле Земли:

.

Здесь М_з – масса Земли, R- радиус Земли, m_т –масса тела.

Обозначим величину (некоторая константа). Если сбросить тело с небольшой высоты вблизи поверхности Земли, то можем записать по второму закону Ньютона:

.

Отсюда следует, что:

.

Опыт показывает (это, в частности, установил Галилей), что a=g, следовательно .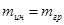

Это равенство установлено экспериментально с относительной погрешностью 10^-12.

4. Основные законы небесной механики.

Законы Ньютона основаны на законах небесной механики, открытых Иоганном Кеплером. Кеплер обработал гигантский материал астрономических наблюдений датчанина Тихо Браге, которые он проводил в течение 35 лет.

Первый закон Кеплера.

Все планеты движутся по эллипсам, в одном из фокусов которых находится Солнце.

Второй закон Кеплера.

Радиус-вектор планеты, проведенный из Солнца, описывает равные площади в равные промежутки времени (рис. 18).

Рис. 18.

Третий закон Кеплера.

Квадраты периодов обращения двух планет вокруг Солнца относятся как кубы больших полуосей их эллиптических орбит.

.

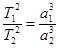Ньютон открыл свой закон всемирного тяготения путем анализа законов Кеплера в приближении круговых орбит планет, вращающихся вокруг Солнца.

Эти законы позволяют получить выражение, с помощью которого можно рассчитать массу Солнца. Из третьего закона Кеплера следует, что для всех планет, при условии движения по круговым орбитам, выполняется следующее соотношение:

.

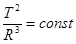Величина этой константы зависит от массы Солнца следующим образом:

.

С помощью этого же соотношения можно рассчитать массу Земли, если в качестве R и T взять радиус лунной орбиты и период ее обращения вокруг Земли.

Ньютон понял, что законы Кеплера верны в приближении неподвижности Солнца (одного из взаимодействующих тел). В действительности планета и Солнце вращаются вокруг их общего центра масс. Возникает возмущающее влияние одного тела на другое (например, Солнца на Землю), и тело начинает рыскать по своей орбите во время движения.

1. Неинерциальные системы отсчета.

Как нам известно, взаимодействие вызывает силу, которая, в свою очередь, вызывает ускорение. Эта цепочка справедлива в инерциальных системах отсчета, в которых выполняются законы механики Ньютона. До сих пор, например, мы считали Землю инерциальной системой отсчета (так называемой, лабораторной), т.е. не принимали во внимание вращение Земли вокруг собственной оси. Посмотрим, к чему же приводит рассмотрение движения тел в неинерциальных системах отсчета. При переходе к неинерциальным системам отсчета ускорение тел в них будет изменяться, а силы, вызванные взаимодействием с окружающими телами, останутся прежними.

1. Силы инерции. Прямолинейное ускоренное движение системы отсчета. Принцип эквивалентности Эйнштейна.

Рассмотрим следующий пример. Пусть вагон движется равноускоренно с ускорением вправо (см. рис. 19):

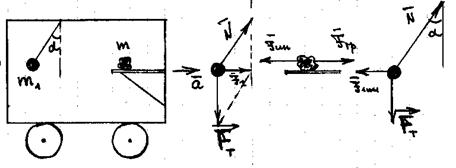Рис. 19

В вагоне на столе находится груз массой m и тело на нити массой m₁. Рассмотрим сначала Землю в качестве лабораторной системы отсчета (инерциальной), а система отсчета, связанная с ускоренно движущимся вагоном, будет неинерциальной. В инерциальной системе отсчета на тело m₁ действуют сила тяжести и сила упругой реакции нити, а на тело m действует сила тяжести, сила упругой реакции стола и сила трения со стороны стола. В инерциальной системе тело m₁ движется ускоренно под действием равнодействующей двух сил – силы тяжести и силы реакции нити, тело m также движется ускоренно под действием силы трения.

В неинерциальной системе вагона тело m₁ покоится, но это не может быть объяснено наличием не скомпенсированной равнодействующей сил. Тело m также не должно покоится из-за наличия не скомпенсированной силы трения. Таким образом, в неинерциальной системе отсчета перестают действовать законы Ньютона. Поступим чисто формально для «спасения» законов Ньютона. Введем в неинерциальной системе отсчета силы инерции, модуль которых равен произведению массы тела на ускорение неинерциальной системы отсчета, а направление силы противоположно направлению этого ускорения:

.

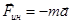Если тело относительно неинерциальной системы отсчета имеет ускорение 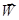, то уравнение движения его в этой системе отсчета имеет вид:

.

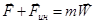Здесь - силы, действующие на тело в инерциальной системе отсчета.

Качественно ответ на вопрос о происхождении сил инерции дает общая теория относительности Эйнштейна. Рассмотрим опыт, известный под названием маятник Любимова (рис. 20).

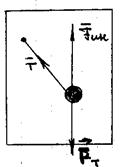Рис. 20.

Маятник Любимова представляет собой доску, в которую вбит гвоздь с укрепленным на нем маятником. При свободном падении маятника он либо начинает вращаться по окружности вокруг точки подвеса, либо остается в покое (если он в момент начала падения находился в отклоненном состоянии). Из рис. 20 видно, что сила инерции компенсирует силу тяжести в неинерциальной системе. Можно сделать следующий вывод:

Если система отсчета находится в равноускоренном прямолинейном движении относительно инерциальной системы отсчета (в которой по определению отсутствуют поля тяготения), то явления в ней протекают так, как если бы имелось поле тяготения, ускорение свободного падения в котором равно ускорению системы отсчета.

Это утверждение и представляет собой принцип эквивалентности Эйнштейна.

Можем теперь уточнить причину возникновения сил в физике:

1. Наличие взаимодействий.
2. Ускоренное движение системы отсчета.

3. Вращательное движение системы отсчета. Тело покоится относительно неинерциальной системы отсчета. Центробежная сила инерции. Влияние вращения Земли на вес тела.

Рассмотрим поведение неподвижного тела во вращающейся системе отсчета. Допустим, что тело лежит неподвижно на поверхности горизонтально расположенного диска, вращающегося с постоянной угловой скоростью 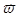(рис. 21).

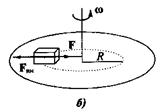Рис. 21.

Покой тела относительно вращающегося диска (неинерциальной системы отсчета) можно объяснить наличием силы инерции, по модулю равной и направленной по радиусу от центра диска. Эту силу инерции называют центробежной силой инерции.

Учтем неинерциальность Земли, как системы отсчета. Поскольку Земля вращается в своем суточном движении вокруг оси, все точки на ее поверхности обладают центростремительным ускорением и, следовательно, Земля не может быть строго инерциальной системой отсчета. Это приводит к следующим следствиям. Рассмотрим некоторое тело, неподвижно лежащее на поверхности Земли. Расставим силы, действующие на него в неинерциальной системе отсчета Земли (рис.22).

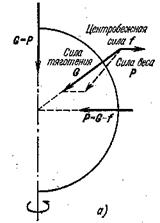Рис. 22

Здесь 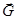- сила гравитационного взаимодействия тела и Земли, направленная к центру Земли по радиусу. 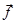- центробежная сила инерции, направленная по радиусу окружности, которую описывает тело при суточном вращении Земли. Векторная сумма этих двух сил и составляет так называемую силу тяжести, которая описывает взаимодействие тела с Землей. Видно, что направление силы тяжести несколько не совпадает с направлением силы гравитационного взаимодействия. Отвес, например, будет висеть не по направлению силы гравитационного взаимодействия, а по направлению силы тяжести.

4. Вращательное движение системы отсчета. Тело движется относительно вращающейся системы отсчета. Силы Кориолиса.

Пусть к оси горизонтально расположенного, вращающегося с угловой скоростью 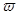диска, прикреплена пружина, на другом конце которой расположено некоторое тело, вращающее относительно диска с линейной скоростью . Окружность, которую описывает тело на диске, имеет радиус R. Запишем ускорение частицы относительно некоторой неподвижной системы отсчета (это будет центростремительной ускорение):

.

Мы использовали закон сложения скоростей Галилея и проделали элементарные математические преобразования.

Видно, что - есть центростремительное ускорение тела в неинерциальной системе отсчета, связанное с вращением тела относительно диска, 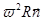- ускорение тела, связанное с вращением диска относительно оси, величина же 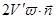- имеет физический смысл ускорения и связана с движение тела относительно неинерциальной системы отсчета (диска). Происхождение этого ускорения свяжем с новой силой инерции, возникающей при движении тела относительно вращающейся системы отсчета, и назовем эту силой Кориолиса. Модуль силы Кориолиса равен .

Общий вид силы Кориолиса можно записать как:

.

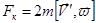Выводы.

1. Сила Кориолиса – сила инерции, возникающая при движении тела относительно вращающейся системы отсчета.

2. Сила Кориолиса перпендикулярна плоскости, в которой расположены векторы и .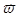

На рис. 23 расставлены силы, действующие на тело в этом случае движения.

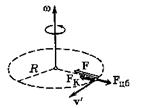Рис. 23.

Сила Кориолиса влияет на движение тел на поверхности Земли, а также движущихся вблизи поверхности Земли. При свободном падении сила Кориолиса отклоняет падающее тело к востоку. При падении на экваторе с высоты 30 м отклонение составляет 3,6 мм. При стрельбе из орудий на дальние расстояния сбудет также учитывать влияние силы Кориолиса. При выстреле из орудия, направленного на север, снаряд будет отклоняться к востоку. У рек, текущих на север, подмываются всегда правые берега. Наличием сил Кориолиса объясняется вращение плоскости колебания маятника Фуко.

Дата добавления: 2014-01-04