Перечень задач для решения при усвоении материала

Во всех задачах обязательным является построение математических моделей, указание экономического смысла переменных, приведение расчетов и подробное описание результата решения задачи.

1 ТЕМА. «ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ».

Задача 1.1.

Предприятие планирует выпускать n видов продукции П_i (i= 1, 2, …, n). При её изготовлении используются ресурсы Р₁, Р₂, и Р₃. прямые затраты ресурсов ограничены соответственно величинами b₁, b₂, и b₃. Расход j-го ресурса (j= 1, 2, 3) на единицу продукции i-го вида составляет a_ij ед. Цена единицы продукции i-го вида равна С_i денежных единиц.

Требуется:

1.Составить математическую модель прямой и двойственной задачи. Раскрыть экономический смысл всех переменных, принятых в задаче;

2.Симплексным методом рассчитать план выпуска продукции по видам с учетом имеющихся ограничении ресурсов, который обеспечивал бы предприятию максимальный доход;

3.Используя решение исходной задачи и соответствия между прямыми и двойственными переменными, найти параметры оптимального плана двойственной задачи;

4.Указать наиболее дефицитный и недефицитный (избыточный) ресурс, если он имеется;

5.С помощью двойственных оценок y_j обосновать эффективность оптимального плана, сопоставить оценку израсходованных ресурсов и максимальный доход. Z_max от реализации готовой продукции по всему оптимальному плану и по каждому виду продукции отдельно;

6.Оценить целесообразность приобретения Dbk единиц ресурса K по цене C_k.

Необходимые исходные числовые данные приведены в табл. 1.1.

Задача 1.2.

Составить диету включающие белки, жиры и углеводы в количестве не менее b_i (i = 1, 2, 3). Для составления смеси можно использовать три вида продуктов B_j (j = 1, 2, 3), содержащую белки жиры и углеводы в количестве a_ij. Цена продуктов C_j. Необходимо определить такой набор продуктов, который обеспечил бы необходимое содержание питательных веществ, и полная стоимость его при этом была бы наименьшей.

Требуется:

1.Составить математическую модель прямой и двойственной задач. Раскрыть экономический смысл всех переменных, принятых в задаче;

2.Симплекс – методом решить двойственную задачу;

Необходимые исходные числовые данные приведена в табл. 1.2.

Табл. 1.1.

Параметр	Номер варианта
а11
а12
а13
а21
а22
а23
а31					5
а32
а33
b1
b2
b3
С1
С2
С3
K
Dbk
Сk

Таблица 1.2.

Параметр	Номер варианта
b1
b2
b3
а11
а12
а13
а21
а22
а23
а31
а32
а33
С1
С2
С3

2 ТЕМА. «ТРАНСПОРТНАЯ ЗАДАЧА»

Задача 2.1

В пунктах А_i (i=1, 2, 3)производится однородная продукция в количестве а_i единиц. Себестоимость единицы продукции в i-м пункте равна C_i. Готовая продукция поставляется в пункты В_j (j=1, 2, 3, 4), потребности которых составляют b_j ед. стоимость перевозки единицы продукции из пункта A_i в пункт B_j задана матрицей C_ij.

Требуется:

1.Написать математическую модель прямой и двойственной задач с указанием экономического смысла всех переменных;

2.Составить план перевозки продукции, при котором минимизируются суммарные затраты по ее изготовлению и доставке потребителям для условия что продукция произведенная в пункте A_i, где себестоимость её производства наименьшая, распределяется полностью;

3.Вычислить суммарные минимальные затраты Z_min;

4.Узнать в какие пункты развозится продукция от поставщиков;

5.Установить пункты, в которых останется нераспределенная продукция, и указать её объем.

Необходимые исходные числовые данные приведены в таблице 2.1.

Задача 2.2.

Трудовые бригады Б₁, Б₂, Б₃ численностью, а₁, а₂, и а₃ человек, сформированы для уборки картофеля.

Для уборки картофеля на четырех полях П₁, П₂, П₃ и П₄ необходимо выделить b₁, b₂, b₃, и b₄ работников. Производительность труда работника зависит от урожайности картофеля, а так же от численности бригады и характеризуется для указанных бригад и полей элементами матрицы P_ij (в центнерах на человека за рабочий день).

Требуется:

1.Распределить работников каждой трудовой бригады по полям так, чтобы за рабочий день было убрано максимально возможное количество картофеля;

2.Определить сколько центнеров картофеля будет убрано с четырех полей при оптимальном распределении работников.

Необходимые исходные числовые данные приведены в таблице 2.2.

Таблица 2.1.

Параметр	Номер варианта
а1
а2
а3
С1
С2
С3
b1					296
b2
b3
b4
С11
С12
С13
С14
С21
С22
С23
С24
С31
С32
С33
С34

Таблица 2.2.

Параметр	Номер варианта
А1
А2
А3
B1
B2
B3
B4					41
Р11
Р12
Р13
Р14
Р21
Р22
Р23
Р24
Р31
Р32
Р33
Р34

3 ТЕМА. «ЦЕЛОЧИСЛЕННОЕ ПРОГРАММИРОВАНИЕ»

Задача 3.1.

Решить задачу методом ветвей и границ. Данные необходимые для решения, приведены в табл. 3.1.

Таблица 3.1

Вариант	Математическая модель задачи
Целевая функция	Ограничения	Условие неотрица-тельности
			x1, x2 ≥ 0
			x1, x2 ≥ 0
			x1, x2 ≥ 0
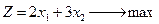
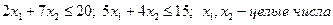
			x1, x2 ≥ 0
			x1, x2 ≥ 0
			x1, x2 ≥ 0
			x1, x2 ≥ 0
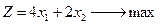
			x1, x2 ≥ 0
			x1, x2 ≥ 0
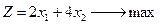
			x1, x2 ≥ 0

Дата добавления: 2014-01-04