Многомерные задачи оптимизации

До сих пор мы обсуждали одномерные задачи оптимизации, в которых целевая функция зависела только от одного аргумента. Однако подавляющее большинство реальных задач оптимизации, представляющих практический интерес, являются многомерными: в них целевая функция зависит от нескольких аргументов, причем, иногда их число может быть, весьма большим.

Математическая постановка таких задач аналогична их постановке в одномерном случае: ищется наименьшее (наибольшее) значение целевой функции, заданное на некотором множестве Е возможных значений ее аргументов. В случае, когда целевая функция непрерывна, а множество Е является замкнутой ограниченной областью, остается справедливой теорема Вейерштрасса. Тем самым выделяется класс задач оптимизации, для которых гарантировано существование решения. В дальнейшем мы всегда будем предполагать, что все рассматриваемые задачи принадлежат этому классу.

Как и в одномерном случае, характер задачи и соответственно возможные способы решения существенно зависят от той информации о целевой функции, которая нам доступна в процессе ее исследования. В одних случаях целевая функция задается аналитической функцией. Тогда можно вычислять ее частные производные, получать явное выражение для градиента и использовать эту информацию для решения задачи. В других случаях никакой формулы для целевой функции нет, а имеется лишь возможность определить ее значения в любой точке рассматриваемой области (с помощью расчетов, в результате эксперимента и т. п.). В таких случаях в процессе решения мы фактически можем найти значения целевой функции лишь в конечном числе точек и по этой информации приближенно установить ее наименьшее значение для всей области.

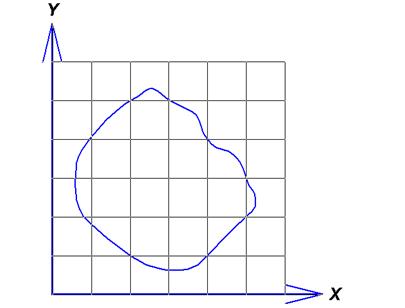
Рисунок 5.4

Многомерные задачи, естественно, являются более сложными и трудоемкими, причем трудоемкости их решения возрастают при увеличении

их размерности. Для примера возьмем самый простой по идее приближенный метод поиска наименьшего значения. Покроем рассматриваемую область сеткой с шагом h (рисунок 5.4) и определим значения функции в ее узлах.

Сравнивая полученные числа между собой, найдем среди них наименьшее и примем его приближенно за наименьшее значение функции для всей области. Однако для задач большой размерности он практически непригоден из-за слишком большого времени, необходимого для проведения расчетов. Иногда сплошной перебор заменяют случайным поиском. В этом случае точки сетки просматриваются не подряд, а по случайному закону. В результате поиск наименьшего значения ускоряется, но теряет свою надежность.

Перейдем к обсуждению методов, позволяющих вести поиск наименьшего значения функции целенаправленно.

Дата добавления: 2014-01-04