Специальные методы

Метод распределения точек по отрезку, учитывающий результаты вычисления целевой функции

Распределяя точки x_k равномерно, мы уделяем одинаковое внимание всем участкам отрезка: тем, где целевая функция велика и тем, в направлении которых она убывает, т. е. не используем информацию о функции f(x), которую мы получаем по мере вычисления чисел y_k = f(x_k).

Организацию вычислений по такой схеме можно сравнить с поведением в лесу неопытно грибника. В поисках грибов он ходит по всему лесу, не чувствуя разницы между грибными и негрибными местами. Опытный же грибник подолгу задерживается на грибных местах, а через негрибные места проходит быстро, не тратя на них лишнего времени.

Чтобы организовать поиск наименьшего значения функции по методу «опытного грибника», нужно отказаться от равномерного распределения точек, а выбирать очередную точку с учетом информации, которую мы получили о функции f(x) в результате ее вычисления в предыдущих точках. При этом основанное внимание следует уделять тем участкам отрезка [a, b], где вычисления дают малые значения функции, просматривая другие участки более бегло. Реализовать эту идею можно, например, следующим образом.

Вычислим значения функции f(x) в двух граничных точках x₀ = a и x₁ = b: y₀ = f(x₀), y₁ = f(x₁). После этого следующую точку x₂ выберем ближе к тому концу отрезка, на котором функция принимает меньшее значение. Ее положение определим соотношением между числами y₀ и y₁: чем больше разница, тем сильнее будет сдвиг точки х₂ в соответствующую сторону. Точку х₃ выберем с учетом взаимного расположения точек x₀, x₁, x₂ и соотношения между числами y₀, y₁, y₂ и т. д. Мы не будем останавливаться на описании возможных алгоритмов выбора очередной точки x_k по информации, полученной в результате вычисления целевой функции на предыдущих шагах – это специальный вопрос, исследования в данной области продолжаются, алгоритмы совершенствуются, и рано говорить об окончательном решении задачи.

До сих пор, обсуждая задачи оптимизации, мы говорили об универсальных методах их решения. Однако во многих случаях из характера задачи вытекает какая-то дополнительная информация о свойствах целевой функции. Это может быть использовано для разработки специальных алгоритмов. Такой подход позволяет существенно сократить объем вычислений и получить ответ наиболее эффективным способом.

В качестве примера рассмотрим случай, когда нам известно заранее, что целевая функция y = f(x) имеет на отрезке [a, b] только один минимум. График такой функции показан на рисунке 5.3.

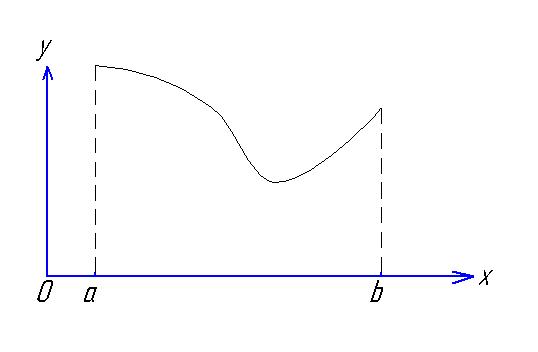
Рисунок 5.3.

Для решения задачи в этом случае можно воспользоваться следующим методом. Возьмем некоторый шаг h и будем последовательно вычислять значения функции f(x) в точках x₀ = a, x₁ = a + h, сравнивая получаемые числа y₀, y₁,… Сначала они будут убывать: y₀ > y₁ > y₂ … Однако в дальнейшем найдется точка x_k = y₀ + kn, где будет справедливо неравенство y_k-1 < y_k, y_k+1 ≥ y_k. Это означает, что наименьшее значение функции достигается на отрезке [x_k-1, x_k+1] и его приближенно можно считать равным y_k = f(x_k). Если требуемая точность в решении задачи еще не обеспечена, то нужно уменьшить шаг h и повторить описанную процедуру для отрезка [x_k-1, x_k+1].

Дата добавления: 2014-01-04