Метод равномерного распределения точек по отрезку

Идея этого метода наиболее проста и естественна. Возьмем некоторое число (целое) n, вычислим шаг h = (b – a) / n и определим значения функции f(х) в точках x_k = a + kn (k = 0, 1, …, n): y_k = f(x_k). После этого найдем среди полученных чисел наименьшее:

m_n = min (y₀, y₁, …, y_n) = min f(x), x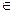[a, b]

Число m_n можно приближенно принять за наименьшее значение функции f(х) на отрезке [a, b]. Благодаря непрерывности функции имеем f(х)

,

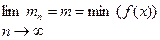т. е. с увеличением числа точек n ошибка, которую мы допускаем, принимая m_n за m стремится к нулю. В этом методе нас может ожидать неприятность, которую иллюстрирует рисунок 5.2.

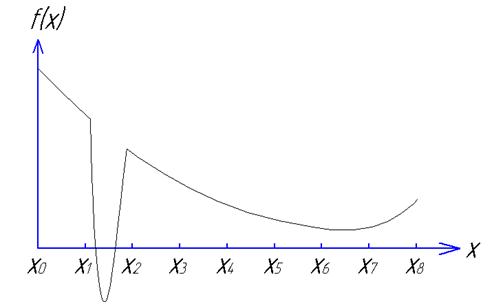
Рисунок 5.2.

На нем приведен график некоторой непрерывной функции. Допустим, что, желая найти ее наименьшее значение, мы взяли m = 8. Определяя значения функции y_k = f(x_k) в точках x_k (k = 0, 1, …, 8) получим

m₈ = min (y₀, y₁, …, y₈) = y₆ = f(x₆)

В данном случае из-за недостаточного числа точек мы пропустим «узкий язык» между х₁ и х₂ , который опускается гораздо ниже y₆ = f(x₆). Поэтому при решении вопроса о числе точек важно максимально полно использовать всю дополнительную информацию о свойствах целевой функции, о степени ее гладкости, вытекающую из характера и особенностей задачи. Не последнюю роль играет и такой фактор, как опыт, интуиция исследователя.

Дата добавления: 2014-01-04