Одномерные задачи оптимизации

Задача о наилучшей консервной банке

Задачи оптимизации

Проектирование сложных РЭС всегда должно быть направлено на поиск наилучшего варианта с точки зрения намеченной цели.

Многие задачи оптимизации сводятся к отысканию наименьшего (или наибольшего) значения некоторой функции, которую принято называть ЦЕЛЕВОЙ. Постановка задачи и методы исследования существенно зависят от свойств целевой функции и той информации о ней, которая может считаться доступной в процессе решения, а также, которая известна априори (до начала решения задачи).

Наиболее простым является случай, когда целевая функция задается явной формулой и является при этом дифференцируемой функцией. В этом случае для поиска экстремальных точек может быть использована производная. Однако, во многих случаях, целевая функция не задается формулой, ее значения могут быть получены в результате сложных расчетов, браться из эксперимента и о. д. Такие задачи являются более сложными, поэтому для них нельзя провести исследование целевой функции с помощью производной. Следует также отметить, что сложность задачи существенно зависит от размерности целевой функции, т. е. от числа ее аргументов.

Тем не менее, рассмотрим сначала случай одномерной оптимизации, во-первых, на нем легче понять постановку вопроса, методы решения и возникающие трудности. Во-вторых, алгоритмы решения многомерных задач оптимизации часто сводятся к последовательному, многократному решению одномерных задач.

Пусть перед нами поставлена задача: указать наилучший вариант консервной банки фиксированного объема V, имеющий обычную форму прямого кругового цилиндра.

Рассмотрим два варианта целевой функции (критерия оптимизации):

1) наилучшая банка должна иметь наименьшую поверхность S (на ее изготовление уйдет наименьшее количество жести);

2) наилучшая банка должна иметь наименьшую длину швов ℓ (швы нужно сваривать и мы хотим минимизировать трудоемкость этой операции).

Для решения этой задачи запишем формулы для объема банки, ее поверхности и длины швов:

V = πr²h, S = πr²+ 2πrh, ℓ=4πr + h (5.1)

Объем банки задан, это устанавливает связь между радиусом r и высотой h. Выразим высоту через радиус: h = V/(πr²) и подставим полученное выражение в формулы для поверхности и длины швов. В результате получим:

S (r) = 2πr² + 2V/r, 0 < r < ∞ (5.2)

ℓ (r) = 4πr + V/πr², 0 < r < ∞ (5.3)

Таким образом, с математической точки зрения, задача о наилучшей консервной банке сводится к определению такого значения r, при котором достигает своего наименьшего значения в одном случае функция S (r), в другом – функция ℓ (r).

Рассмотрим первый вариант задачи. Вычислим производную функции S’ (r):

S’ (r) =4πr - 2V/r² = 2/r² (2πr³ – V) (5.4)

Своего наименьшего значения эта функция достигает в точке r = r₁, в которой ее производная обращается в нуль. Как не трудно убедиться:

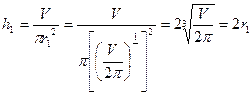; (5.5)

При этом

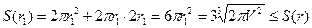(5.6)

Рассмотрим теперь задачу во второй постановке. Продифференцируем функцию ℓ (r).

ℓ’ (r) = 4π – 2V/πr³ = 2/ πr²(2 π²r² – V) (5.7)

Приравняв производную нулю, получим, что радиус и высота банки, наилучшие с точки зрения критерия минимальности ℓ(r), определяются формулами

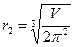, h₂ = 2πr₂, (5.8)

при этом

. (5.9)

Мы видим, что при разных критериях оптимизации получаются существенно разные ответы.

Рассмотрим общие вопросы постановки и методов решения одномерных задач оптимизации. С математической точки зрения такую задачу можно сформулировать следующим образом.

Найти наименьшее (или наибольшее) значение целевой функции f(x), заданной на множестве Х. Определить значение переменной 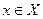, при котором она принимает свое экстремальное значение.

В математическом анализе при изучении свойств функций, непрерывных на отрезке, доказывается следующая теорема.

ТЕОРЕМА ВЕЙЕРШТРАССА. Всякая функция f(x), непрерывная на отрезке [a, b], принимает на этом отрезке свое наибольшее и наименьшее значение, т. е. на отрезке [a, b] существуют такие точки x₁, x₂, что для любого выполняются неравенства

f(x₁) ≤ f(x) ≤ f(x₂) (5.10)

Не исключается, в частности, возможность того, что наименьшее или наибольшее значение достигается сразу в нескольких точках. В этом легко убедиться, рассмотрев в качестве примера функцию y = sin (x) на отрезке [0, 4π]. Она достигает своего минимального значения, равного -1, сразу в двух точках x = 3π/2, x = 7π/2. Наибольшее значение, равное 1, достигается также в двух точках: x = π/2, x = 5π/2.

Теорема Вейерштрасса играет в данном случае роль теоремы существования: согласно этой теореме задача оптимизации, в которой целевая функция f(x) задана и непрерывна на отрезке, всегда имеет решение.

Теперь нам предстоит обсудить методы решения задач оптимизации. При их исследовании мы будем предполагать, что целевая функция f(x) дифференцируема на отрезке [a, b] и имеется возможность найти явное выражение для ее производной f’(x).

Функция f(x) может достигать своего наименьшего или наибольшего значения либо в одной из двух граничных точек отрезка [a, b], либо в какой-нибудь его внутренней точке. В последнем случае такая точка обязательно должна быть экстремальной. Учитывая изложенное, можем сформулировать следующее правило решения задачи оптимизации для рассматриваемого класса функций.

Для того чтобы определить наибольшее и наименьшее значение дифференцируемой на отрезке [a, b] функции f(x), нужно найти все ее экстремальные точки на данном отрезке, присоединить к ним граничные точки a, b и во всех точках сравнить значения функции. Наименьшее и наибольшее из них дадут наименьшее и наибольшее значения функции для всего отрезка.

Поскольку граничные точки a, b искать не надо, то с технической точки зрения все сводится к определению экстремальных точек, которые являются корнями уравнения

f’(x) = 0. (5.11)

Для иллюстрации изложенного правила решения задачи оптимизации рассмотрим на отрезке [-2, 3] функцию

f(x) = 3x⁴ – 4x³ – 12x² + 2 (5.12)

Вычислим ее производную:

f’(x) = 12x³ – 12x² – 24x

Таким образом, уравнение (2.62) для определения экстремальных точек принимает вид

x³ – x² – 2x = 0 (5.13)

Все корни этого уравнения: x₁ = -1; x₂ = 0; x₃ = 2 принадлежат исходному отрезку. Добавляя к ним граничные точки: a = -2 и b = 3, вычислим соответствующие значения функции (2.63):

f(-2) = 34, f(-1) = -3, f(0) = 2, f(2) = -30, f(3) = 29.

Из сравнения этих чисел следует, что наименьшее значение функции f(x) достигается в одной из экстремальных точек х = 2, а наибольшее – в граничной точке х = -2, причем

f_min = f(2) = -30,

f_max = f(-2) = 34.

График функции иллюстрирующий проведенное исследование, изображён на рисунке 5.1.

Рисунок 5.1.

5.3. Численное решение одномерных задач оптимизации

Рассмотрим следующий пример. Химический завод производит некоторое вещество. Выход интересующего нас продукта определяется температурой: y = f(T). Температуру можно варьировать в определенных пределах: T₁ ≤ T ≤ T₂. Вид функции f заранее неизвестен, но зависит от используемого сырья. Получив очередную партию сырья, нужно найти температуру T, при которой наиболее выгодно вести производство, т. е. функция f(T) достигает своего наибольшего значения.

С математической точки зрения мы имеем типичную одномерную задачу оптимизации. В то же время между этой задачей и задачей о консервной банке имеется существенное различие. В данном случае нет никакой формулы для целевой функции f(T). Чтобы определить ее значение при некоторой температуре Т, нужно провести опыт в лаборатории (если это возможно), либо прямо в производственных условиях. Совершенно ясно, что возможно лишь конечное число измерений и тем самым функция f(T) будет известна нам в конечном числе точек. Значений ее производных мы вообще определить не можем. Остается добавить, что каждое измерение требует времени, а задерживать производство нельзя. Поэтому необходимо получить ответ на поставленный вопрос после небольшого числа измерений, т. е. по значениям функции y = f(T) в нескольких точках.

Итак, обсудим математические вопросы, связанные со следующей постановкой одномерной задачи оптимизации, определяя значение непрерывной функции f(х) в некотором конечном числе точек отрезка [a, b], нужно приближенно найти ее наименьшее (или наибольшее) значение на данном отрезке.

Рассмотрим разные подходы к решению этой задачи.

Дата добавления: 2014-01-04