
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Булевы уравнения
|
|
|
|
Примером булева уравнения с одним неизвестным может служить соотношение Х (А
(А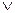 В)=А
В)=А В
В С, где Х- некоторая булева функция, зависящая от А,В,С, которую необходимо найти, чтобы в результате подстановки Х(А,В,С) в данное соотношение, оно обращалось бы в тавтологию.
С, где Х- некоторая булева функция, зависящая от А,В,С, которую необходимо найти, чтобы в результате подстановки Х(А,В,С) в данное соотношение, оно обращалось бы в тавтологию.
Перейдем от элементов Х,А,В,С к их изображающим числам. Относительно базиса b[А,В,С] найдем #АВС=00000001; #(А+В)=01110111 и, следовательно #Х должно быть таким, чтобы выполнялось равенство
(01110111) (#Х)=00000001,
(#Х)=00000001,
откуда #Х=*000*001, где вместо (*) можно записать как 0 так и 1. Таким образом, рассматриваемое уравнение имеет 4 решения, соответствующие изображающим числам 00000001; 10000001; 00001001; 10001001, т.е. Х1=А В
В С, Х2=А
С, Х2=А В
В С
С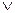 ¬А
¬А ¬В
¬В С, Х3=С
С, Х3=С (А
(А В
В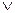 ¬А
¬А ¬В), Х4=¬А
¬В), Х4=¬А ¬В
¬В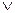 А
А В
В С.
С.
4.4.2.4 – замена переменных. Понятие замены переменных в алгебре логики аналогично понятию замены переменных в обычной алгебре.
Пример. Преобразовать элементы А и В в элементы А1 и В1:
А=А1 В1
В1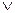 ¬А1
¬А1 ¬В1; В=¬А1.
¬В1; В=¬А1.
Вычислим по отношению к базису b[А1,В1] изображения числа #A и #B
#А1=0 1 0 1, #¬А1=1 0 1 0,
#В1=0 0 1 1, #¬В1=1 1 0 0.
Значения столбцов 0 1 2 3
Тогда
#A =0001+1000=1001
#B = 1010
Значения столбцов 3021
Как видно из примера переход от одних переменных к другим сводится к перестановке столбцов в изображающих числах переменных. Перестановка столбцов может быть описана с помощью перестановочной булевой матрицы Rij
|| Fkj ||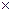 || Rij ||=|| Gkj ||, (4.4)
|| Rij ||=|| Gkj ||, (4.4)
где || Fkj || - матрица, составленная из набора изображающих чисел переменных А1 и В1, || Gkj || - матрица, составленная из набора изображающих чисел переменных А и В в базисе [А1,В1]. Заполняя (4.4) конкретным содержанием в соответствии с вышеприведенным примером
i= 0123 j=3021

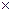
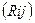 =
=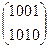 (4.5)
(4.5)
Из (4.5) следует, что столбец с номером i=0 переводится в столбец с номером j=1, столбец с номером i=1 переводится в столбец с номером j=3, столбец с номером i=2 ставится на место столбца с номером j=2, и столбец с номером i=3 смещается на место столбца с номером j=0. Это значит, что в перестановочной матрице || Rij || элементы с указанными значениями индексов i и j равны 1, а остальные равны 0, т.е.
Rij=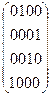 (4.6)
(4.6)
Вернемся к нашему примеру с наблюдениями разведчика. Сравнивая значения столбцов в соотношениях (4.2) и (4.3) можно придти к заключению о том, что один набор изображающих чисел может быть получен из другого перестановкой столбцов двумя способами. Это означает, что существует два различных решения, которые можно определить, если найти соответствующую замену переменных, переводящую левый набор функций в правый и наоборот.
Исследуем решение, при котором единичными элементами перестановочной матрицы || Rij || являются R02=1, R15=1, R26=1, R31=1, R43=1, R54=1, R67=1, R70=1. Тогда
|| Rij || = 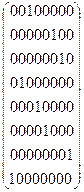
и искомое преобразование переменных

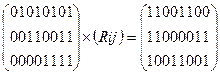 #А=
#А=
#В=
#С=
откуда
#А[А1,В1,С1] = (11001100),
#В[А1,В1,С1] = 11000011, (4.6)
#С[А1,В1,С1] = 10011001
что в соответствии с вышеупомянутыми рассуждениями дает следующее решение булевых уравнений:
а) А =¬В1; в) В = В1 С1
С1 ¬В1
¬В1 ¬С1; с) С = А1
¬С1; с) С = А1 В1
В1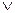 ¬А1
¬А1 ¬В1.
¬В1.
Обратное преобразование переменных осуществляется матрицей
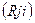 =
=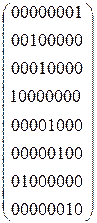
И имеет вид
 #А1=
#А1=
#В1=
#С1=
откуда
#А1[А,В,С] = (01011010),
#В1[А,В,С] = (10101010),
#С1[А,В,С] =(01100110), что соответствует следующим соотношениям:
d) А1 = А ¬С
¬С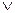 ¬А
¬А С; e) В1=¬А; g) C = А
С; e) В1=¬А; g) C = А ¬В
¬В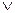 ¬А
¬А В.
В.
Последние соотношения допускают следующую интерпретацию:
а) на плоской местности будет применяться легкая артиллерия; b) в ночное время противник будет применять дальнобойную артиллерию и тяжелые танки или же легкую артиллерию без танков; c) при плохой погоде либо будет предпринято наступление пехоты на широком фронте, поддержанное дальнобойной артиллерией, либо будут проводиться локализованные атаки пехоты, сопровождаемые огнем легкой артиллерии; d) наступление на широком фронте будет предпринято или на плоской местности при хорошей погоде или на холмистой местности при плохой погоде; e) тяжелые танки будут применяться на плоской местности в дневное время или на холмистой местности ночью.
Используя полученные результаты ответим на вопрос: какова будет тактика противника, если битва будет происходить на равнине в ясный день?
А¬В¬С=¬В1 (В1
(В1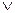 С1)
С1)  (¬В1
(¬В1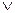 ¬С1)
¬С1) (А1
(А1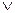 В1)
В1)  (¬А1
(¬А1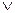 ¬В1)=
¬В1)=
=¬В1 (¬В1
(¬В1 С1
С1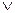 ¬В1
¬В1 ¬С1)
¬С1) (¬В1
(¬В1 А1
А1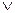 ¬А1
¬А1 ¬В1)=А1
¬В1)=А1 ¬ В1
¬ В1 С1.
С1.
В последнем случае использована теорема де Моргана
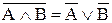

Следовательно, в таком сражении будет применено наступление пехоты на широком фронте, поддержанное легкой артиллерией и тяжелыми танками.
Второй вариант решения, когда единичными элементами перестановочной матрицы ||Rij||, будут R02=1, R15=1, R27=1, R31=1, R43=1, R54=1, R66=1, R70=1, предлагается найти самостоятельно.
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 2578; Нарушение авторских прав?; Мы поможем в написании вашей работы!