Предмет и задачи психодиагностики. Задача об использовании ресурсов

Задача об использовании ресурсов

Траекторная задача

Линейное программирование.

В этом подразделе мы познакомимся с линейным программированием. Так называются задачи оптимизации, в которых целевая функция является линейной функцией своих аргументов, а условия, определяющие их допустимые значения, имеют вид линейных уравнений и неравенств. Исторически линейной программирование развиваться начало в первую очередь в связи с задачами экономики, с поиском способов оптимального распределения и использования ресурсов. Оно послужило основой широкого использовании математических методов в экономике. Следует подчеркнуть, что в рамках реальных экономических задач число независимых переменных обычно бывает очень большим (тысячи, десятки тысяч аргументов). Поэтому практическая реализация алгоритмов решения таких задач принципиально невозможна без использования современной вычислительной техники. Рассмотрим в качестве примера линейного программирования так называемую транспортную задачу.

В городе имеются два склада муки и два хлебозавода. Ежедневно в первого склада вывозится 50 т. муки. Со второго 70т. Первый завод использует 40т. второй 80т. Допустим, что перевозка одной тонны муки с первого склада на первый завод стоит 1р 20ком., с первого склада на второй завод – 1р 60коп., со второго склада на первый завод – 80коп. и со второго склада на второй завод – 1р. Как нужно спланировать перевозки, чтобы их стоимость была минимальной?

Для того, чтобы ответить на этот вопрос дадим математическую постановку задачи. Обозначим через х1 и х2 количество муки, которую следует с первого склада соответственно на первый и второй заводы, а через х3 и х4 количество муки, которую нужно перевезти со второго склада на первый и второй заводы. Эти условия приводят к системе уравнений

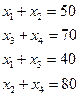(5.14)

Первые два уравнения системы определяют, сколько муки нужно вывести с каждого склада, два других показывают, сколько муки нужно привезти на каждый завод. Очевидно полагаем, что в обратном направлении с заводов на склады муку не возят =)). Общая стоимость перевозок определяется формулой

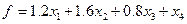(5.15)

С математической точки зрения задача заключается в том, чтобы найти числа 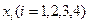, и удовлетворяющие условиям (5.14) и минимизирующие стоимость перевозок (5.15).

Рассмотрим систему (5.14). Это система четырёх уравнений с четырьмя неизвестными. Однако независимыми в ней являются только первые три уравнения, 4-е – их следствие (если сложить 1-е и 2-е уравнение и вычесть 3-е, получится 4-е). Таким образом, фактически нужно рассмотреть следующую систему, эквивалентную (5.14):

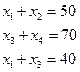(5.16)

В ней число уравнений на единицу меньше числа неизвестных, так что мы можем выбрать какую-нибудь неизвестную х₁ и выразить через нее с помощью уравнений (5.16) три остальных. Соответствующие формулы имеют вид:

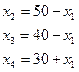(5.17)

Учитывая, что 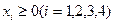, получаем систему

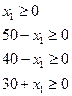(5.18)

Из которой следует

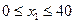(5.19)

Таким образом, задавая любое х₁, удовлетворяющее (5.19) и вычисляя х₂,х₃,х₄ по формулам (5.17) мы получим один из планов перевозки. При реализации этого плана с каждого склада будет вывезено и на каждый завод доставлено нужное количество муки.

Вычислим стоимость перевозок. Для этого подставим (5.17) в формулу (5.16). В результате получаем

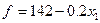(5.20)

Эта формула определяет величину f как функцию одной переменной 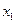, которую можно выбирать произвольно в пределах ограничения (5.19).

Очевидно, что стоимость окажется минимальной, когда 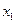примет максимально возможное значение 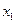=40. Значение остальных величин 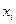находится по формулам 5.17

Итак, оптимальный по стоимости план перевозок имеет вид

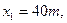
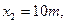
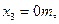
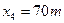(5.21)

Стоимость перевозок в этом случае составит 134р. При любом другом допустимом плане перевозок она окажется выше f>fmin=134.

Мебельная фабрика выпускает стулья двух типов. Но изготовление одного стула первого типа стоимостью 8р., расходуется 2м. досок стандартного сечения, 0,5 м2 обивочной ткани и 2 чел/ч рабочего времени. Для стульев второго типа аналогичные данные: 12р, 4м, 0,25 м2 и 2.5 чел/ч.

Допустим, что в распоряжении фабрики имеется 440м досок, 65м2 обивочной ткани, 320 чел/ч рабочего времени. Какое количество стульев каждого типа надо изготовить, чтобы в рамках этих ресурсов стоимость произведенной продукции была максимальной?

Для ответа на этот вопрос постараемся опять сформулировать задачу как математическую. Обозначим через х₁ и х₂ запланированной к производству число стульев соответственно первого и второго типов. Ограниченный запас сырья и трудовых ресурсов означает, что х₁ и х₂ должна удовлетворять неравенствам

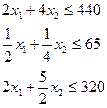(5.22)

Кроме того, по смыслу задачи они должны быть неотрицательными:

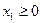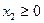, (5.23)

Стоимость запланированной к производству продукции определяется формулой

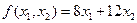(5.24)

Итак, с математической точки зрения задача составления оптимального по стоимости выпущенной продукции плана фабрики сводится к определению пары целых чисел х₁ и х₂, удовлетворяющих линейным неравенствам (5.22) (5.23) и дающих наибольшее значение функции (5.24). Мы опять получили типичную задачу линейного программирования.

Для анализа сформулированной задачи рассмотрим плоскость и введем на ней декартову систему координат х₁,х₂. Найдем на этой плоскости множество точек, координаты которых удовлетворяют (5.22) и (5.23). Неравенства (5.23) означают, что это множество лежит в первой четверти. Выясним теперь смысл ограничений, которые задаются неравенствами (5.22)

Проведем на плоскости прямую, определяемую уравнением

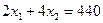(5.25)

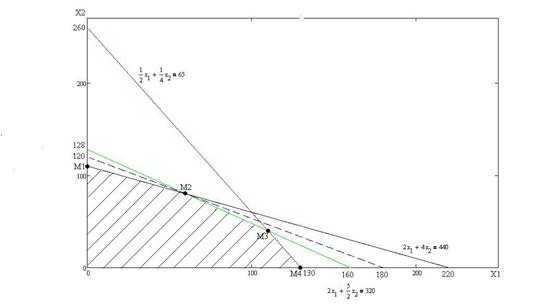
Рисунок 5.10

Она делит плоскость на две полуплоскости. На одной из них, расположенной ниже прямой (5.25) функции 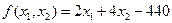принимает отрицательные значения на второй, расположенной выше прямой (5.25) – положительные. Таким образом первое из неравенств (5.22) выполняется на множестве точек, которые включаются в себя прямую (5.25) и полуплоскость, расположенную ниже этой прямой.

Совершенно аналогично можно найти множества точек, удовлетворяющие второму и третьему неравенствам (см. рисунок 5.10).

Возьмем пересечение трех найденных множеств и выделим его часть, расположенную в первой четверти. В результате получим множество точек, удовлетворяющих всей совокупности ограничений (5.22) (5.23). Данное множество имеет вид пятиугольника, заштрихованного на рисунке 5.10. Его вершинами являются точки пересечения прямых, на которых неравенства (5.22) и (5.23) переходят в точные неравенства. Координаты вершин пятиугольника указаны на рисунке 5.10.

Любой точке Р с целочисленными координатами (х₁, х₂), принадлежащей данному пятиугольнику, соответствующий план выпуска стульев, который может быть выполнен при имеющихся запасах сырья и трудовых ресурсов (реализуемый план). Наоборот, если точка Р не принадлежит пятиугольнику, то соответствующий план не может быть выполнен (нереализуемый план)

Рассмотрим на плоскости х₁, х₂ линии уровня целевой функции (5.24)

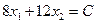(5.26)

Это уравнение описывает семейство прямых, параллельной прямой

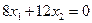(5.27)

При параллельном переносе этой прямой вправо параметр С возрастает, влево – убывает. Отсюда важный вывод: оптимальный план должен располагаться на прямой семейства (5.27), наиболее удалённой от начала координат.

Этот вывод позволяет закончить решение задачи. Посмотрим на рисунок 5.10. На нем воспроизведен пятиугольник реализуемых планов. Наиболее удаленной от центра в этом пятиугольнике является точка М₂ с координатами (60, 80).

Итак, оптимальный план найден – он предписывает производство 60 стульев первого типа и 80 стульев второго типа. Стоимость этой продукции 1440р. На выполнение плана нужно затратить 440м досок, 50 м² обивочной ткани, 330 чел/ч рабочего времени.

Как видно, оптимальный план требует полного использования запаса досок и трудовых ресурсов, в то время как обивочная ткань будет израсходована не полностью – останется 15 м².

Этот результат ясен из рисунка 5.10. Точка М₂, определяющая оптимальный план, является вершиной многоугольника. Она лежит на пересечении прямых

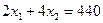
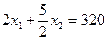
Уравнение этих прямых получаются из первого и третьего условий системы (5.22) при замене их на строгие равенства. Это означает полный расход их на строгие равенства. Это означает полный расход досок и трудовых ресурсов. Однако точка М2 не принадлежит прямой

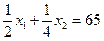
так что второе условие (5.22) связанное с ограниченным запасом обивочной ткани имеем в ней форму неравенства

50<65.

Проведенный анализ показывает, что дальнейшее увеличение стоимости продукции регламентируется запасом досок и трудовых ресурсов.

Психодиагностика - область психологической науки, разрабатывающая методы выявления и измерения индивидуально-психологических особенностей личности.

Психодиагностика - раздел психологического знания, формирующегося на стыке фундаментальных областей психологии с практическими запросами жизни.

Психодиагностические методики - один из инструментов научных исследований в психологии личности и межличностных отношений.

В каждой из этих областей существуют специфические условия использования психодиагностических средств, специфические психодиагностические задачи и методы, составляющие предмет частных или специальных психодиагностик.

Выделяют и более общие, универсальные вопросы, решение которых закладывает фундамент любой специальной психодиагностики. Эти вопросы составляют предмет общей психодиагностики. К ним относятся:

1. методологические, теоретические и конкретно- методические принципы построения психодиагностических инструментов и формулирования психодиагностических заключений.

2. методы и конкретные методики психодиагностики наиболее универсальных объектов психодиагностических обследований, таких, как черты личности, способности, мотивы, сознание и самосознание, межличностные отношения.

3. дифференциальная психометрика как математизированная методология обнаружения межиндивидуальных различий.

4. нормативные требования к методикам, их разработчикам и пользователям.

Основными функциями психодиагностики являются:

1. осуществление контроля за формированием необходимых знаний, умений и психических функций

Психодиагностика позволяет:

1 более эффективно осуществлять отбор детей для коррекционной работы с психологом

2 дальнейшее развитие психических функций, способностей и умений детей

3 проводить необходимую коррекцию учебно-воспитательного процесса с учетом индивидуальных психологических особенностей детей

Главной целью психодиагностики является обеспечение полноценного психического и личностного развития. Также сюда входит создание условий для проведения прицельной коррекционно - развивающей работы, выработки рекомендаций, проведения психотерапевтических мероприятий и т.д.

Дата добавления: 2014-01-04