Проблема многоэкстремальности

Для иллюстрации проблемы посмотрим рисунок 5.9 и сравним его с 5.5-5.8. Первые рисунки относятся к функциям, имеющим только один минимум.

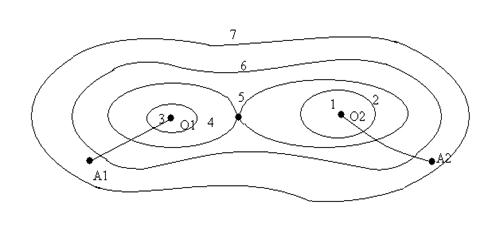
Рисунок 5.9.

Поэтому откуда бы ни начинался поиск, мы придем в конце концов к нужной точке. На рисунке 5.9 приведены линии уровня функции с двумя локальными максимума в точках О1 и О2. Такие функции принято называть многоэкстремальными. Сравнивая между собой значения функции в точках О1 и О2: f1=3, f2=1, находим, что наименьшее значение функция достигается в точке О2.

Представьте себе теперь, что, не имея перед глазами рисунке 5.9 и не зная о многоэкстремальности функции, мы начали поиск наименьшего значения с помощью метода градиентного спуска из точки А1. Очевидно, что поиск приведет нас к точку О1, которую ошибочно можно принять за исковый ответ. С другой стороны, если мы начнем поиск с точки А2, то окажется на правильном пути и быстро придем в точку О2.

Как бороться с многоэкстремальностью. Универсального ответа на этот вопрос нет. Самый просто прием состоит в том, что проводят поиск несколько раз и начиная его с разных точек. Если при этом получаются разные ответы, то сравнивают в них значения целевой функции и выбирают наименьшее. Расчета останавливают после того, как несколько новых поисков не меняют полученного ранее результата. Выбор начальных точек поиска, обоснованность прекращения расчетов в значительной степени зависят от опыта и интуиции специалистов, решающих задачу.

Нарисованная картина может показаться слишком мрачной. На самом деле во многих случаях имеется различная дополнительная информация о характере задачи, которая существенно помогает при выборе метода, начальной точки поиска и т.п. Кроме того, пока мы не делали никаких предположений о специальных свойствах целевой функции и о характере рассматриваемой области. Это затрудняет анализ. Конкретизация задачи, выделение определенных классов функций и области позволяет провести более глубокое исследование и разработать специальные методы, которые решают задачу исчерпывающим образом. Важным классом таких «специализированных» задач оптимизации являются задачи линейного программирования. Существуют и другие типы задач оптимизации являются задачи линейного программирования. Существуют и другие типы задач оптимизации однако на них мы останавливаться не будем.

Дата добавления: 2014-01-04