Метод наискорейшего спуска

Вычисление градиента на каждом шаге, позволяющее все время двигаться в направлении наиболее быстрого убывания целевой функции, может в то же время замедлять вычислительный процесс. Дело в том, что подсчет градиента – обычно гораздо более сложная операция, чем подсчет самой функции. Поэтому часто пользуются модификацией градиентного метода, получившей название метода наискорейшего спуска.

Согласно этому методу после вычисления в начальной точке градиента функции делающей в направлении антигравитации не меленький шаг, а движутся до тех пор, пока функция убывает. Достигнув точки минимум на выбранном направлении, снова вычисляют градиент функции и повторяют описанную процедуру. При этом градиент вычисляется гораздо реже, только при смене направления движения.

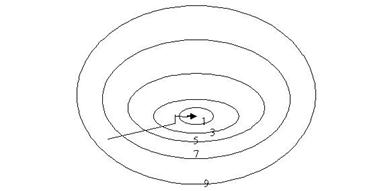
Рисунок 5.7

На рисунке 5.7 показана траектория поиска наименьшего значения целевой функции по методу наискорейшего спуска для функции, аналогичной изображенной на рисунках 5.5-5.6 это траектория ведет к цели не так быстро, как на рисунке 5.6 экономия машинного времени за счет более редкого вычисления градиента может быть весьма существенной.

5.4.4. Проблема «оврагов»

Мы рассмотрели три варианта методов спуска и показали, как хорошо они работают. Однако всё было хорошо, потому что был выбран «удобный» пример. Но давайте рассмотрим пример функции, изображенной на рисунке 5.8

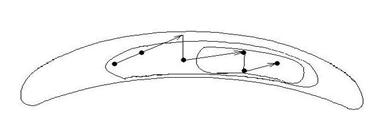
Рисунок 5.8

На нем также показаны линии уровня некоторой функции однако их реконфигурация отличается от рисунков 5.5-5.7 Линии уровня сильно вытянуты в одном направлении и сплющены в другом. Они напоминают рельеф местности с оврагом. Этот случай крайне неудобен для описанных выше методов.

Действительно, попытаемся найти наименьшее значение такой функции с помощью градиентного спуска. Двигаясь все время в направлении антиградиента, мы быстро спустимся на дно оврага и, поскольку движение идет хотя и маленькими, по конечными дискретными шагами, проскочим его. Оказавшись на противоположной стороне оврага и вычислив там градиент функции, мы будем вынуждены развернуться почти на 180 градусов и сделать один или несколько шагов в обратном направлении. При этом мы снова проскочим дно «оврага» и вернемся на его первоначальную сторону. Продолжая этот процесс, мы вместо того, чтобы двигаться по дну «оврага» в сторону его понижения, будем совершать зигзагообразные скачки поперёк «оврага», почти не приближаясь к цели. Таким образом, в случае «оврага» (этот математический термин прочно закрепился в литературе) описанные выше методом оказываются неэффективными.

Для борьбы с оврагами был предложен ряд приемов. Один из них заключается в следующем. Из двух близких точек совершают градиентный спуск на дно «оврага». Потом соединяют найденные точки прямой и делают вдоль неё большой «овражный» шаг. Из найденной точки снова спускаются на дно «оврага» и делают второй овражный шаг (соединив эту точку с предыдущей, из которой делался первый «овражный» шаг). В результате, двигаясь достаточно быстро вдоль «оврага», приближается к искомому наименьшему значению целевой функции. Такой метод достаточно эффективен для функции двух переменных, однако при большем числе переменных могут возникнуть трудности.

Все описанные выше методы приспособлены к случаю, когда наименьшее значение функции достигается внутри рассматриваемой области, и становятся малоэффективными, если наименьшее значение достигается на границе или вблизи неё. Для решения этих задач приходится разрабатывать специальные методы. Мы не будем на них останавливаться. Одно должно быть ясно-большое число специальных методов- признак слабости а не силы математических методов.

Дата добавления: 2014-01-04