Характеристики иерархической структуры программной системы

Сложность программной системы

В простейшем случае сложность системы определяется как сумма мер сложности ее модулей. Сложность модуля может вычисляться различными способами.

Например, М. Холстед (1977) предложил меру длины N модуля [33]:

N»n₁ log ₂(n₁)+n₂ log ₂(n₂),

где n₁ – число различных операторов, n₂ – число различных операндов.

В качестве второй метрики М. Холстед рассматривал объем V модуля (количество символов для записи всех операторов и операндов текста программы):

V=N ´ log ₂(n₁+n₂).

Вместе с тем известно, что любая сложная система состоит из элементов и системы связей между элементами и что игнорировать внутрисистемные связи неразумно.

Том МакКейб (1976) при оценке сложности ПС предложил исходить из топологии внутренних связей [49]. Для этой цели он разработал метрику цикломатической сложности:

V(G)=E - N +2,

где Е – количество дуг, а N – количество вершин в управляющем графе ПС.

Это был шаг в нужном направлении. Дальнейшее уточнение оценок сложности потребовало, чтобы каждый модуль мог представляться как локальная структура, состоящая из элементов и связей между ними.

Таким образом, при комплексной оценке сложности ПС необходимо рассматривать меру сложности модулей, меру сложности внешних связей (между модулями) и меру сложности внутренних связей (внутри модулей)[28],[56]. Традиционно со внешними связями сопоставляют характеристику «сцепление», а с внутренними связями – характеристику «связность».

Вопросы комплексной оценки сложности обсудим в следующем разделе.

Иерархическая структура программной системы – основной результат предварительного проектирования. Она представляет состав модулей ПС и управляющие отношения между модулями. В этой структуре модуль более высокого уровня (начальник) управляет модулем нижнего уровня (подчиненным).

Иерархическая структура не отражает процедурные особенности программной системы, то есть последовательность операций, их повторение, ветвление и т.д. Рассмотрим основные характеристики иерархической структуры, представленной на рис. 1.17.

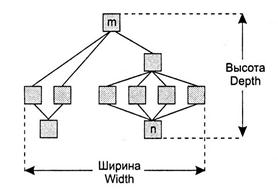
Рис 1.17 Иерархическая структура программной системы

Первичными характеристиками являются количество вершин (модулей) и количество ребер (связей между модулями). К ним добавляются две глобальные характеристики – высота и ширина:

- высота – количество уровней управления;

- ширина – максимальное из количеств модулей, размещенных на уровнях управления.

В нашем примере высота=4, ширина=6.

Локальными характеристиками модулей структуры являются коэффициент объединения по входу и коэффициент разветвления по выходу.

Коэффициент объединения по входу Fan_in(i) – это количество модулей, которые прямо управляют i- м модулем. В примере для модуля n: Fan_in(n)=4.

Коэффициент разветвления по выходу Fan_out(i) – это количество модулей, которыми прямо управляет i- й модуль. В примере для модуля m: Fan_out(m)=3.

Возникает вопрос: как оценить качество структуры? Из практики проектирования известно, что лучшее решение обеспечивается иерархической структурой в виде дерева.

Степень отличия реальной проектной структуры от дерева характеризуется невязкой структуры. Как определить невязку? Вспомним, что полный граф (complete graph) c n вершинами имеет количество ребер

e_c=n(n-1)/2,

а дерево (tree) c таким же количеством вершин – существенно меньшее количество ребер

e_t=n-1.

Тогда формулу невязки можно построить, сравнивая количество ребер полного графа, реального графа и дерева.

Для проектной структуры с n вершинами и е ребрами невязка определяется по выражению:

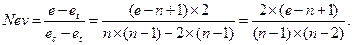
Значение невязки лежит в диапазоне от 0 до 1. Если Nev =0, то проектная структура является деревом, если Nev =1, то проектная структура – полный граф. Ясно, что невязка дает грубую оценку структуры. Для увеличения точности оценки следует применить характеристики связности и сцепления.

Хорошая структура должна иметь низкое сцепление и высокую связность. Л Констентайн и Э. Йордан (1979) предложили оценивать структуру с помощью коэффициентов Fan_in(i) и Fan_out(i) модулей [77].

Большое значение Fan_in(i) – свидетельство высокого сцепления, так как является мерой зависимости модуля. Большое значение Fan_out(i) говорит о высокой сложности вызывающего модуля. Причиной является то, что для координации подчиненных модулей требуется сложная логика управления.

Основной недостаток коэффициентов Fan_in(i) и Fan_out(i) состоит в игнорировании веса связи. Здесь рассматриваются только управляющие потоки (вызовы модулей). В то же время информационные потоки, нагружающие ребра структуры, могут существенно изменяться, поэтому нужна мера, которая учитывает не только количество ребер, но и количество информации, проходящей через них.

С. Генри и Д. Кафура (1981) ввели информационные коэффициенты ifan_in(i) и ifan_out(j) [35]. Они учитывают количество элементов и структур данных, из которых
i- й модуль берет информацию и которые обновляются j- м модулем соответственно.

Информационные коэффициенты суммируются со структурными коэффициентами sfan_in(i) и sfan_out(j), которые учитывают только вызовы модулей.

В результате формируются полные значения коэффициентов:

Fan_in(i)= sfan_in(i)+ ifan_in(i),

Fan_out(j)= sfan_out(j)+ ifan_out(j).

На основе полных коэффициентов модулей вычисляется метрика общей сложности структуры:

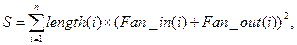
где length(i) – оценка размера i- го модуля (в виде LOC- или FP-оценки).

[1] Боэм Б.У. Инженерное проектирование программного обеспечения: Пер. с англ. – М.: Радио и связь, 1985. – 512 с.

Дата добавления: 2014-01-04