Особенности самоорганизующихся систем

На протяжении нескольких последних десятилетий одним из основных источников новых взглядов на устройство мира стала синергетика, усилия которой изначально направлены на выявление универсальных механизмов устройства и функционирования систем различной природы. Синергетику называют также наукой о сложности, поскольку существование таких универсальных механизмов служит залогом познаваемости сложных систем. Чтобы быть реализуемым, сложное должно быть устроено просто, а простые схемы немногочисленны и потому универсальны.

Под сложностью системы обычно понимают ее принципиальную несводимость к простой сумме своих частей. Как следует из этого определения, сложность неразрывно связана с нелинейностью. В самом деле, к линейной системе применим принцип суперпозиции и ее можно разложить на независимые составляющие, из описания которых легко собирается исходная система. Этим обстоятельством обусловлено еще одно имя синергетики – нелинейная динамика, или – шире – нелинейная наука.

Вехами развития любой научной дисциплины являются ее парадигмы – исходные концептуальные схемы, модели постановки проблем и их решения. К настоящему моменту в синергетике сформировалось три парадигмы.

Первая из них – парадигма самоорганизации. В системах, находящихся вдали от положения равновесия, происходят процессы самоорганизации, приводящие к выделению из множества описывающих систему величин небольшого числа параметров порядка – ведущих переменных, к которым подстраиваются все прочие.

Вторая парадигма синергетики – парадигма динамического хаоса. Это явление представляет собой сложное непериодическое поведение, наблюдаемое в детерминированных системах (т.е. в таких, где будущее однозначно определяется прошлым и настоящим и нет случайных факторов). Основным результатом на этом этапе стало установление факта существования пределов предсказуемости, связанных с наличием горизонта прогноза – конечного времени, через которое динамический прогноз поведения системы становится невозможен.

Третья парадигма синергетики – парадигма сложности, – лежит на стыке двух предыдущих – в каком-то смысле они взяли представление о сложности "в вилку". Если первая и вторая парадигмы связаны, соответственно, с порядком и хаосом, то третью обычно обозначают словосочетанием «жизнь на кромке хаоса» (скольжение вдоль этой кромки).

Базовой моделью теории самоорганизованной критичности является куча песка.

Рассмотрим уголок с песком, изображенный на рис. 1.3.

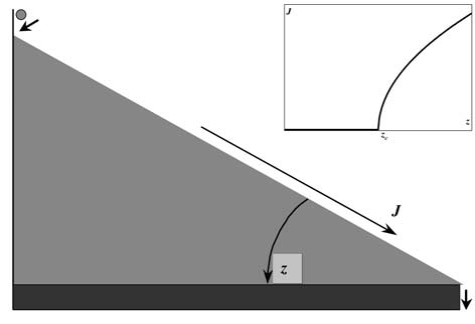
Рисунок 1.3 – Уголок с песком

Состояние песка определяется углом наклона поверхности z. При его изменении происходит непрерывный фазовый переход (зависимость параметра порядка от управляющего параметра приведена на врезке) от неподвижного состояния (J = 0) к состоянию непрерывного тока песка (J > 0). При токе J = +0, соответствующем добавлению одной песчинки за один шаг, система самоорганизуется в состояние с критическим наклоном z = z_c.

Будем предполагать сцепление между песчинками достаточно большим.

При этом возможно лишь поверхностное перемещение песка, причем инерцией его движения можно пренебречь. Тогда состояние системы вполне определяется наклоном поверхности. В тех местах, где локальный наклон оказывается больше порога устойчивости, происходит осыпание, приводящее к соскальзыванию песчинок вниз по склону на соседние участки поверхности.

Если средний наклон поверхности z невелик, то песок неподвижен. Если же наклон превышает некоторое значение zc, возникает спонтанный ток песка J по поверхности, который непрерывно возрастает при увеличении z (см. врезку на рис. 3). То есть, налицо непрерывный фазовый переход, в котором управляющим параметром является наклон z, а параметром порядка – ток песка J.

Критическое значение наклона zc разделяет хаотическую (z < z_c) и упорядоченную (z > z_c) фазы. Обе эти фазы соответствуют некатастрофическому поведению, поскольку в них система устойчива к малым возмущениям. В хаотической фазе они еще быстро затухают во времени и пространстве, а в упорядоченной –уже не могут ощутимо повлиять на величину тока. И лишь в критической точке, где одна добавленная песчинка может вызывать лавину любого размера, возможны катастрофы.

Критическое состояние возникает, когда параметр порядка едва становится ненулевым, т.е. соответствуют моменту его отрыва от нуля. В случае обычных критических явлений такое состояние достигается путем тонкой подстройки. Однако, вместо того чтобы подбирать для управляющего параметра a priori неизвестное критическое значение, можно установить параметр порядка в +0, что заставит управляющий параметр самостоятельно отыскать критическую точку.

Самоорганизации кучи песка в критическое состояние происходит при токе J = +0.

Чтобы обеспечить такую величину параметра порядка, будем рассматривать динамику по шагам, добавляя песчинки по одной на вершину кучи (см. рис. 2) и дожидаясь завершения процесса релаксации. При этом ток песка через систему, очевидно, имеет минимально возможное значение – в среднем одна песчинка за один шаг рассмотрения.

Дата добавления: 2014-01-04