Проблема детерминизма

До недавнего времени (второй половины ХХ века) в математике и физике превалировала идея Лапласа о полной предопределенности развития систем. Считалось, что если знать начальные условия и математическое описание поведения объекта, то можно определить его состояние на любом промежутке времени.

Hапpимеp, если pечь идет о механической системе, то хорошо известно, что задание начальных условий — координат и импульсов — однозначно определяет последующую ее эволюцию. Именно поэтому, во вpемена пpеобладания механистического взгляда на пpиpоду вещей, появилось известное изpечение Лапласа: "Дайте мне начальные условия, и я пpедскажу будущее миpа". Эта увеpенность в пpавоте Лапласа и пpедсказуемости поведения систем, описываемых классической механикой, сохpанялась вплоть до самого последнего вpемени в сознании большинства естествоиспытателей. Однако исследования последних 30 лет произвели настоящую pеволюцию в этой области и показали, что не все так пpосто и что детеpминиpованная механическая система может вести себя совеpшенно непpедсказуемо. И наобоpот, в основе неpегуляpного, хаотического поведения часто лежит вполне детеpминиpованное описание.

В пpиpоде и в повседневной пpактике много таких пpоцессов, котоpые, на пеpвый взгляд, выглядят совеpшенно случайными, а на самом деле являются отражением хаотической динамики.

Как утверждают современные теории, хаос присутствует везде. Завихряется струйка сигаретного дыма, трепещет и полощется флаг на ветру, капли воды из подтекающего крана падают то одна за другой, то словно выжидают. Хаос обнаруживается и в капризах погоды, и в траектории движения летательного аппарата, и в поведении автомобилей в дорожной пробке, и в том, как струится нефть по нефтепроводу. Каковы бы ни были особенности конкретной системы, ее поведение подчиняется одним и тем же недавно открытым закономерностям. Осознание этого факта заставило менеджеров пересмотреть отношение к страховке, астрономов — под другим углом зрения взглянуть на Солнечную систему, политиков — изменить мнение о причинах вооруженных конфликтов.

Однако трудности теоретического анализа хаоса затрудняют построение эффективных моделей. Характерный пример приводится о попытке построить систему математических моделей для анализа биологических проблем. На вопрос, что мешает совместной работе математиков и биологов, исследователи ответили: "Математикам – незнание математики, биологам – незнание биологии".

Зарождение хаоса происходит в результате бифуркаций.

Суть бифуркации лучше всего иллюстрирует витязь на распутье, который стоит перед камнем с надписью "Направо пойти --- женатому быть, налево пойти --- коня потерять, прямо пойти --- буйну голову сложить" (правда, чью голову сложить, обычно не поясняется). В каком-то месте пути попадается развилка, где нужно принимать решения. Около развилки пути еще очень близки, но дальше они ведут витязя к совершенно разным приключениям.

Или можно представить себе балку прямоугольного сечения, на которую положен груз, в точности как показано на рис. 1.1. Кладем сверху гирьки, увеличиваем груз, балка сжимается и остается прямолинейной. Но, начиная с некоторого критического веса, она уже не может оставаться в этом положении и прогибается вправо или влево. Ей приходится "выбирать", куда прогнуться под действием случайных факторов.

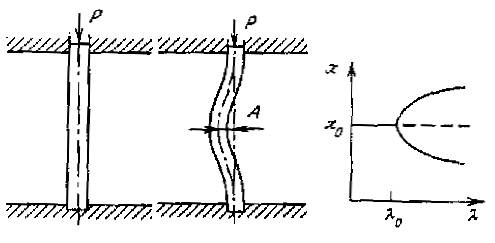
Рисунок 1.1 – Простейший пример бифуркации --- прогиб балки

При значении параметра большем l₀ балка уже не может оставаться прямой. Ей приходится "выбирать" под действием случайных факторов --- прогнуться вправо или влево (сплошным линиям соответствуют устойчивые состояния, пунктирным --- неустойчивые).

Если нарисовать зависимость максимального прогиба балки от массы груза, то получается так, как показано на рис.1.1. Нелинейщики называют такие картинки очень красивым словом --- " бифуркационные диаграммы".

Особенностью бифуркаций является чрезвычайная чувствительность системы к условиям, определяющим ее состояние. Исследователь хаоса Эдвард Лоренц назвал это свойство «эффектом бабочки».

Нелинейщики прекрасно знают, что неустойчивые ветви – вещь очень важная. Они могут коренным образом менять ход устойчивых. Устойчивая и неустойчивая ветвь бифуркационной диаграммы могут столкнуться и аннигилировать. Тогда в системе может произойти катастрофический скачок или революционное изменение.

Никколо Макиавелли в своей книге «Государь» приводит такой факт.

«Сицилиец Агафокл стал царем Сиракуз, хотя вышел не только из простого, но и из презренного звания". Вступив в войско, он выслужился до претора Сиракуз. Утвердясь в этой должности, он задумал сделаться властителем Сиракуз и таким образом присвоить себе то, что было вверено ему по доброй воле. Он созвал однажды утром народ и сенат Сиракуз, якобы для решения дел, касающихся республики, а когда все собрались, то солдаты его по условленному знаку перебили всех сенаторов и богатейших людей из народа. После такой расправы Агафокл стал властвовать, не встречая ни малейшего сопротивления со стороны граждан».

Эта история может быть отображена бифуркационной диаграммой, показанной на рисунке 1.2. В качестве бифуркационного параметра на этом рисунке показана временная переменная λ, характеризующую медленные изменения, а в качестве характеристики состояния системы (аналог прогиба балки) рассматривается степень социальной защищенности населения. Описанная модель прекрасно подходит для тех ситуаций, когда общество действует под влиянием одного человека, который может сказать, что "государство – это я". Такие ситуации многократно возникали в те периоды, когда история государств была историей королей.

Рисунок 1.2 – Бифуркационная диаграмма, которая вполне подходит к истории, описанной Н. Макиавелли

Итак, поведение системы может существенно усложняться вблизи точки бифуркации. В переводах С.Я. Маршака есть иллюстрация такой ситуации (стихотворение написано в 16 веке):

«Не было гвоздя — подкова пропала,

Не было подковы — лошадь захромала,

Лошадь захромала — командир убит,

Конница разбита, армия бежит,

Враг вступает в город, пленных не щадя.

Оттого что в кузнице не было гвоздя».

После двух последовательных бифуркаций система становится хаотичной. В хаотической динамике система описывается сложной траекторией, представляющей собой странный аттрактор. Название «странный» этот аттрактор получил в связи с тем, что в отличие от обычных аттракторов (точка или замкнутая кривая) странный аттрактор имеет незамкнутую траекторию, то есть система не имеет памяти о своем предыдущем движении.

Уместно привести еще одну историю, представленную в Интернете.

Давным-давно, в тридевятом царстве, в тридесятом государстве, в благословенной стране Обормотии, жили-были обормоты. Жили-поживали, горя не знали. Но тут накрыл их вал технического прогресса, и стали они думу думать, что производить — сковородки с экскаваторами или компьютеры с искусственным интеллектом. И решили обормоты, что интеллекта у них и своего хватит, а вот сковородки — дело стоящее. И тут мечты у них в моду вошли и фантазии, о чем — в точности сказать не можем, однако письменность у них вскоре исчезла. Но оказалось, что и со сковородками дела все хуже и хуже, и пошли разговоры о возврате к славным старым временам, к общеобормотным ценностям. Тут обормоты вообще перестали понимать, что же с ними творится, а когда дым рассеялся (в прямом и переносном смысле), оказалось, что превратилась благословенная Обормотия в сырьевой придаток, а соседи обсуждают, жить учат и гуманитарную помощь оказывают.

Представители нелинейной науки не особенно любят признаваться, что многие идеи и проблемы этой области пришли из других дисциплин. В некоторых науках есть задачи, размышления над которыми позволили создать новые разделы математики и нелинейной науки. Например, одной из задач биологии является проблема морфогенеза. Это попытка понять, как в ходе развития организма клетки с одинаковой генетической информацией "узнают", суждено им стать клетками мозга или желудка. Попытка понять этот феномен привела Джона фон Неймана к теории самовоспроизводящихся автоматов, Алана Тьюринга – к новому поколению математических моделей, Рене Том, строя модели морфогенеза, попутно создал прекрасную и чарующую теорию катастроф. И это только вершины. Вся горная цепь намного больше. Сейчас многие "нелинейщики" приходят к выводу, что в XXI в. поставщиком таких сверхзадач станут науки о человеке – психология, политология, социология и прежде всего история.

Завершая обзор особенностей исследования нелинейных систем, уместно упомянуть и такой класс систем, как самоорганизующиеся системы.

Дата добавления: 2014-01-04