Принцип самоподобия фракталов

Рассмотрим несколько примеров на построение множеств с использованием формулы (2.11).

Возьмем отрезок прямой единичной длины (это можно сделать для любого отрезка, приняв длину этого отрезка за единицу, т.к. размерность длины в данном случае не играет никакой роли). Разделим отрезок на 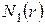равных частей, где 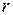– длина каждой части. Каждую часть можно считать копией исходного отрезка, уменьшенной в 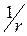раз. Очевидно, что . Назовем исходный отрезок сегментом 0-й итерации (0-го поколения). Ясно, что если мы используем формулу (2.11), то получаем:

,

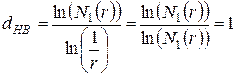то есть исходный отрезок без дополнительных преобразований имеет размерность Хаусдорфа-Безиковича, совпадающую с топологической размерностью.

Поступим теперь по-другому: от исходного отрезка АВ (сегмента 0-й итерации) (рис. 2.2, а) перейдем, например, к образующей 1-й итерации самоподобного фрактала CD, где число сегментов равно 7, а длина каждого отрезка по-прежнему равна 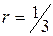, (рис. 2.2, б).

Если теперь использовать формулу (2.11), то получим:

.

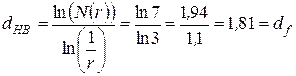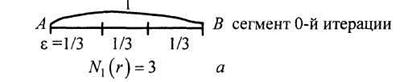
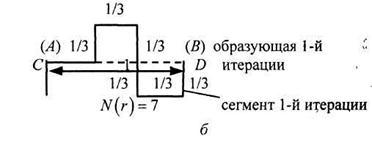
Рисунок 2.2 – Построение образующей самоподобного фрактала с ,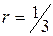

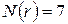
Таким образом, величина 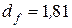(фрактальная размерность самоподобного фрактала с образующей CD) показывает, что кривая CD в 1,81 раза «более извилистая» на отрезке АВ, чем сам отрезок АВ. Можно провести и обратную процедуру, выкидывая, например, часть отрезков длины 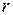из сегмента АВ. В этом случае размерность образующей будет меньше размерности сегмента АВ, то есть .

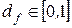Построение самого фрактального множества (самоподобного фрактала) производят последовательным использованием сегмента 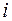-й итерации для образующей () итерации. При получим предельное (фрактальное) множество.

Аналогичный алгоритм используется и для двумерных объектов, например, квадратов. Возьмем квадрат единичной площади (квадрат 0-й итерации) и, разделив каждую сторону на 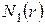равных частей длиной 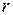, получим N ₂ (r) квадратов, подобных исходному, но имеющих сторону в 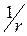раз меньше исходной (рис. 2.3, а). Сформируем образующую 1-й итерации самоподобного фрактала, выкидывая из исходного квадрата 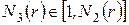квадратов (рис. 2.3, б):

.

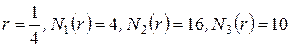Если теперь определить число копий исходного квадрата в образующей 1-й итерации, то оно равно: .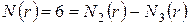

Найдем фрактальную размерность получаемого множества:

.

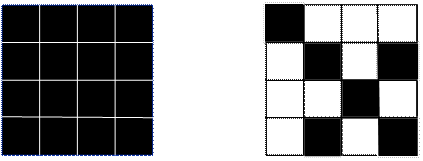
а б

Рисунок 2.3 – Квадрат 0-й итерации, N₂ (r) = 16 (а) и образующая самоподобного фрактала N(r) = 6 (б)

Аналогичную процедуру можно производить над геометрическими объектами размерности .

Из проведенного анализа следует, что для того, чтобы найти размерность самоподобного фрактала, необходимо определить число элементарных мер (пробных функций) 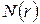образующей 1-й итерации (число подобъектов), вычислить коэффициент подобия 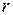и использовать формулу (2.11).

Рассмотрим построение некоторых классических фрактальных множеств.

Дата добавления: 2014-01-04