Система итерированных функций

Как отмечалось ранее, процедура построения фракталов представляет собой итерационный процесс – переход от одного множества к другому. На каждом шаге выполняются преобразования над множеством, полученном на предыдущем шаге. Данный алгоритм можно представить в виде следующей схемы:

(2.17)

Здесь – преобразования, выполняемые на 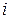-м шаге над множеством (– исходное компактное множество).

На каждом шаге итерационного процесса выполняются однотипные преобразования. В общем же случае на каждом шаге могут выполняться различные преобразования, определяемые следующим образом:

. (2.18)

Преобразования вида (2.18) называются преобразованиями Хатчинсона. Преобразования Хатчинсона позволяют строить разнообразные фракталы за счет выбора элементарных преобразований .

Необходимо отметить, что если преобразования заранее определены, то получаемый результат совершенно не зависит от выбора исходного компактного множества . Кроме того, не любые преобразования Т порождают фракталы.

Если, например, преобразование Хатчинсона получено с использованием двух аффинных преобразований:

,

где

,

,

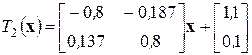то можно построить фрактал под названием «лист» (рис. 2.15).

Рисунок 2.15 – Фрактал «лист»

Если использовать четыре аффинных преобразований вида:

,

,

,

то получим фрактал под названием «кристалл» (рис. 2.16).

Рисунок 2.16 – Фрактал «кристалл»

Задача построения предельного множества Е (аттрактора из исходного компактного множества Е_о) в результате итерационного процесса с заданным преобразованием является прямой задачей. Ее особенностью является то, что вид аттрактора определяется только коэффициентами аффинного преобразования (если такое используется) и не зависит от выбора исходного множества Е_о. В то же время можно поставить обратную задачу, а именно, определить совокупность отображений, для которых заданное множество является аттрактором. Обратная задача значительно сложнее прямой, однако имеет огромное прикладное значение, в частности, в области сжатия изображений.

Необходимость сжатия изображений обусловлена различными факторами. Основными являются:

· разгрузка каналов связи и, соответственно, снижение себестоимости передачи данных;

· экономия памяти компьютеров за счет архивации изображений и др.

Дата добавления: 2014-01-04