Применение случайных фракталов для моделирования

Рассмотренные выше теоретические положения определяют сущность случайных фракталов. Одномерные классические и фрактальные винеровские процессы может быть и не имеют самостоятельного значения при моделировании природных образований, однако являются основой для построения двумерных процессов, с помощью которых можно моделировать естественные ландшафты – горные хребты, лесную поверхность, волнение моря и т.д.

Рисунок 2.20 – Реализации фрактального винеровского процесса

Двумерный фрактальный винеровский процесс (поверхность) определяется следующим образом: – это функция двух аргументов 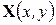, обладающая следующими свойствами:

1) 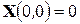и почти все реализации процесса непрерывны;

2) Приращения процесса :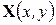

,

где 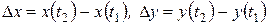– являются случайной величиной, имеющей нормальный интегральный закон распределения.

Фрактальная размерность двумерного винеровского процесса равна:

.

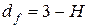На рисунках 2.21-2.23 приведены примеры части фрактальной поверхности (функция max{ X,0}), соответствующие двумерным винеровским процессам с различными значениями параметра 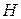. Изменяя значение 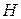, можно моделировать самые разнообразные типы земной поверхности – от равнин до горных хребтов.

Рисунок 2.21 – Двумерный фрактальный винеровский процесс;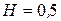

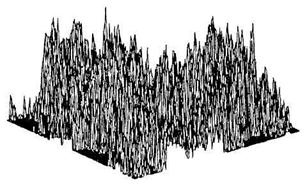
Рисунок 2.22 – Двумерный фрактальный винеровский процесс: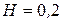

Для моделирования одномерных и двумерных фрактальных винеровских процессов более эффективно использование преобразования Фурье. При этом случайный процесс начинает обладать некоторой памятью, что позволят достигнуть некоторой регулярности на модели процесса.

Моделирование основывается на том, что спектральная плотность фрактального винеровского процесса аппроксимируется степенной функцией 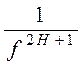, то есть:

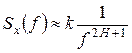, (2.24)

которая убывает при увеличении частоты .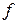

Основная идея моделирования фрактального винеровского процесса состоит в произвольном задании спектральной плотности , сохраняющей требуемые свойства, определенные зависимостью (2.24), и последующем применении обратного преобразования Фурье.

Рисунок 2.23 – Двумерный фрактальный винеровский процесс: Н = 0,8

Моделирование осуществляется на конечном интервале изменения аргумента функции 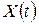, то есть рассматривается функция 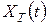. Поскольку используются средства вычислительной техники, то в итоге формируется числовая последовательность 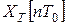, являющаяся дискретной аппроксимацией :

,

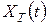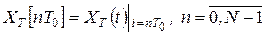где 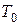– шаг дискретизации процесса, 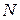– число дискретных отсчетов.

Практическая реализация выполняется следующим образом. Синтезируется дискретное преобразование Фурье для числовой последовательности 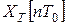в виде:

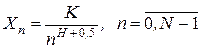. (2.25)

Здесь .

Зависимость (2.25) определяется в данной форме в силу справедливости соотношения (2.24). Поскольку для каждого значения 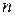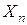является произвольным комплексным числом, то коэффициент 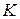можно задать в форме:

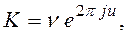(2.26)

где 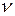– значение нормально распределенной случайной величины с нулевым математическим ожиданием и единичной дисперсией, 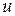– значение равномерно распределенной случайной величины на отрезке [0,1].

К синтезированному комплексному вектору 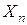применяется обратное дискретное преобразование Фурье. Результатом является искомая числовая последовательность .

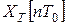При построении случайных фрактальных поверхностей двумерных фрактальных винеровских процессов используются те же процедуры, что и в одномерном случае. В отличие от одномерного случая вместо вектора 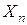вначале синтезируется двумерная матрица 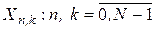, удовлетворяющая условию:

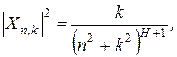(2.27)

а затем применяется двумерное обратное преобразование Фурье.

Дата добавления: 2014-01-04