Методы определения фрактальной размерности временных рядов

Существуют несколько подходов к определению фрактальной размерности:

1) Клеточная размерность;

2) поточечная размерность;

3) корреляционная размерность;

4) информационная размерность.

Клеточная размерность. Используется при исследовании размерности линий и площадей с фрактальной природой.

Её суть заключается в том, что линия или площадь накрывается сеткой с размером ячейки . Затем подсчитывается количество клеток 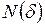, накрывающих исследуемую линию (или площадь). Далее величина несколько раз уменьшается и для каждого нового значения определяется соответствующее количество клеток 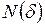. На рисунке 2.24 приведена иллюстрация этого процесса.

В результате этого получаем несколько пар значений 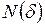–, для которых вычисляем логарифмы.

Теперь построим систему координат в двойном логарифмическом масштабе 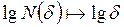и нанесем точки с координатами [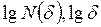] на плоскости. Проведем прямую линию через эти точки, как показано на рисунке 2.25.

Далее определим угол наклона этой линии 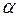, как показано на рисунке 2.26. Клеточная фрактальная размерность представляется выражением:

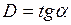. (2.28)

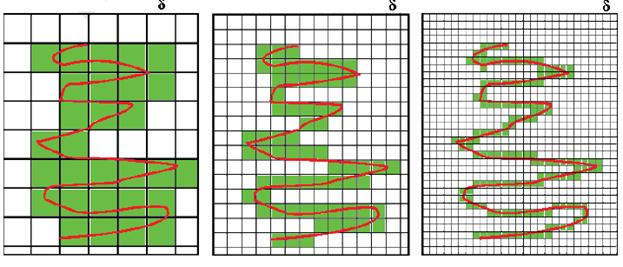
Рисунок 2.24 – Покрытие кривой линии клетками с различными размерами

Рисунок 2.25 – Построение системы координат с двойным логарифмическим масштабом

Поточечная (фрактальная) размерность. Рассмотрим какую-нибудь траекторию в фазовом пространстве на протяжении длительного времени (рис. 2.27).

Проведем выборку точек на траектории (достаточно большое число N_o) произвольным образом. Опишем вокруг какой-нибудь точки х₀ на траектории сферу диаметра 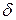(или куб с ребром 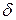) и подсчитаем число выборочных точек 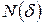, попавших внутрь сферы.

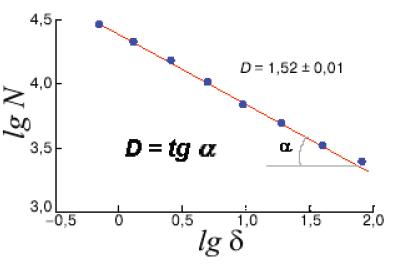
Рисунок 2.26 – Определение клеточной фрактальной размерности по наклону прямой линии

Вероятность того, что выборочная точка окажется внутри сферы, определяется выражением:

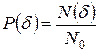, (2.29)

где 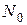– общее число точек на траектории.

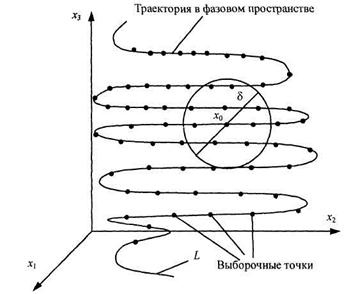
Рисунок 2.27 – Геометрические построения для нахождения поточечной (фрактальной) размерности

Размерность траектории для некоторой области точек 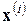фазового пространства имеет вид:

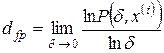. (2.30)

Несмотря на то, что формула (2.30) отличается от общей формулы (2.11) по определению фрактальной размерности, тем не менее выражение (2.30) можно привести к (2.11).

Пусть длина всей кривой L равна 1 (это всегда можно допустить). Пусть 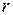– расстояние между отдельными точками. Тогда 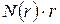, где 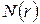– число точек, попавших в сферу, определяет длину кривой 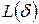в сфере диаметра 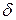, a .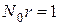

Имеем:

.

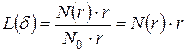Рассмотрим отрезок 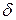(диаметр сферы). Если вновь принять длину этого отрезка за 1, то число отрезков, покрывающих длину 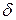=1, определится как 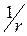, в то же время число отрезков, покрывающих 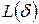, равно:

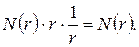
Тогда:

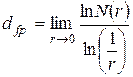
и мы получим исходную формулу (2.11).

Как видно, здесь вновь использовался основной принцип – принцип самоподобия фракталов. Для многих фракталов это определение не зависит от 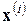, но для других аттракторов 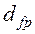зависит от 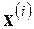, поэтому лучше воспользоваться усредненной поточечной размерностью.

Выберем случайным образом множество точек М <N₀ и в каждой точке вычислим 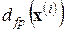, после чего определим усредненную поточечную размерность:

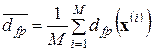. (2.31)

Корреляционная (фрактальная) размерность. Эта размерность широко используется для определения меры упорядоченности движений и является нижней оценкой хаусдорфовой размерности странного аттрактора.

На первом этапе определяется корреляционный интеграл 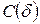по формуле:

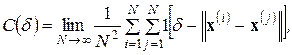(2.32)

где 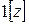– функция Хевисайда; 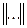– какая-либо норма.

Функция Хевисайда представляет собой единичную ступенчатую функцию, которая приобретает значение 1 в момент 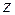. Применение функции Хевисайда позволяет обнаружить момент, когда мера переходит из нуля к бесконечности.

Норма – это правило, означающее, что сопряжённым алгебраическим числам соответствует некоторое рациональное число.

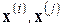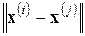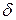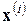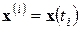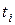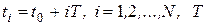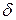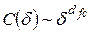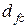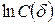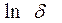Фактически двойная сумма в (2.32) определяет число пар , расстояние между которыми не превышает . Предполагается, что – вектор, описывающий положение изображающее точки в фазовом пространстве в момент времени , где – некоторый заданный промежуток времени. При малых корреляционный интеграл , поэтому корреляционную размерность можно определить по наклону зависимости от или:

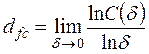. (2.33)

В случае изучения скалярной динамической системы или одной координаты вектора состояния 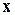фрактальную размерность можно определить с помощью процедуры Паккарда-Такенса.

Пусть 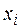– реализация одной из координат фазового пространства системы 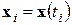. Введем в рассмотрение новое фазовое пространство (пространство вложения размерности р), точки которого определяются векторами 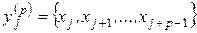, сконструированными из последних значений величин 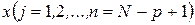. При изменении 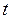получим в этом пространстве траекторию, воспроизводящую некоторое множество, корреляционная размерность которого 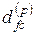может быть вычислена через корреляционный интеграл:

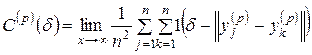. (2.34)

Фрактальная размерность определяется по наклону зависимости 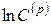от 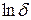, или:

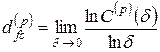. (2.35)

Изменяя размерность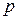векторов у, проанализируем зависимость 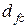от 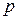(кривую Паккарда-Такенса). Оказывается, что размерность 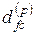сростом 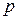увеличивается. Однако если регистрируемый сигнал есть проявление детерминированного хаоса, то при некотором 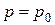величина 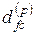перестает расти (!). Достигнутое при этом значение 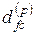принимается за размерность 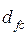исходной системы. Если же рост 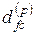продолжается без насыщения, то это свидетельствует о том, что наблюдаемый сигнал шумовой (!).

Таким образом, обычный случайный процесс можно рассматривать как движение системы на аттракторе бесконечной размерности. Конечная размерность аттрактора означает, что данный сигнал можно воссоздать с помощью динамической системы.

Это особенно важно при решении задач управления, когда необходимо отличать детерминированный хаос от обычных шумов и помех. Дело в том, что наличие внутреннего порядка в детерминированном хаосе позволяет в принципе управлять им, в то время как шумовой хаос неуправляем.

Покажем, что минимальное число динамических переменных, необходимое для описания наблюдаемого хаотического движения, оценивается как 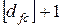, где [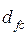] – целая часть фрактальной размерности. Эта оценка может быть использована, в частности, для решения одной из самых сложных задач, возникающих при идентификации модели рассматриваемой системы, – задачи определения количества динамических параметров, необходимых для описания системы.

Рассмотрим примеры, связанные с применением процедуры Паккарда-Такенса. Первый и второй примеры иллюстрирует идентификацию размерности математической модели, третий – диагностику объекта управления, третий.

Пример 1. На рисунке 2.28 представлены графики пульсации давления глубинного насоса для различных жидкостей, полученные с помощью тензодатчиков с глубины 390 метров.

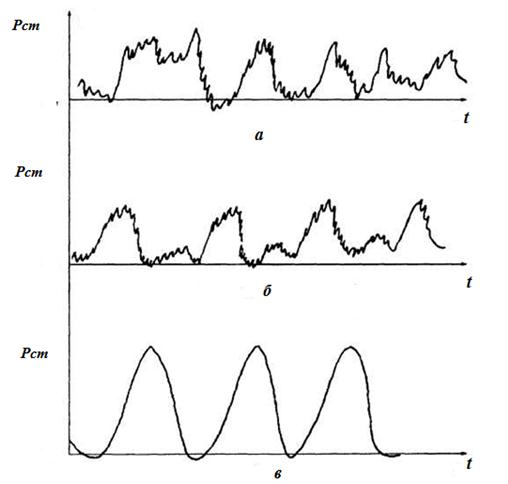
Рисунок 2.28 – Пульсация давления в скважине: 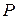– давление,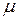- вязкость, Р_ст - статическое давление, а -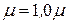, Па с (вязкость пластовой воды); б – 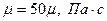(дегазированная нефть), в – 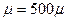, Па с (водоэмульсионная смесь)

Как видно из рисунка 2.28, при большой вязкости (рис. 2.28,в) начинаются периодические колебания с периодом, равным продолжительности одного цикла качания насоса. С уменьшением вязкости 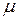движения усложняются и можно предположить, что устанавливаются хаотические колебания при малых 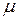(рис 2 28, а).

Проверка этой гипотезы выполнена процедурой Паккарда-Такенса. На рисунке 2.29 построена зависимость корреляционной размерности 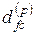от размерности 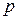вектора 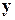. Из рисунка видно, что при 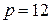наступает насыщение 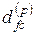. Следовательно, в данном случае действительно наблюдается детерминированный хаос, причем [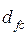] = 3, поэтому минимальное число динамических переменных, необходимых для описания наблюдаемых колебаний, равно 4.

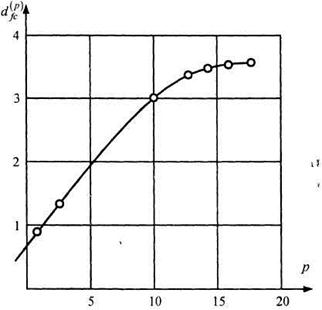
Рисунок 2.29 – Построение кривой Паккарда-Такенса для выявления хаоса и определения фрактальной размерности ()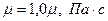

Пример 2. В работе [9] приводятся результаты исследования выделения сейсмической энергии землетрясений в различных диапазонах магнитуд (от 3 до 8 баллов) с использованием каталогов землетрясений Японских островов. Графики зависимости фрактальных размерностей 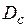от размерностей пространства вложения 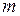приведены на рисунке 2.30.

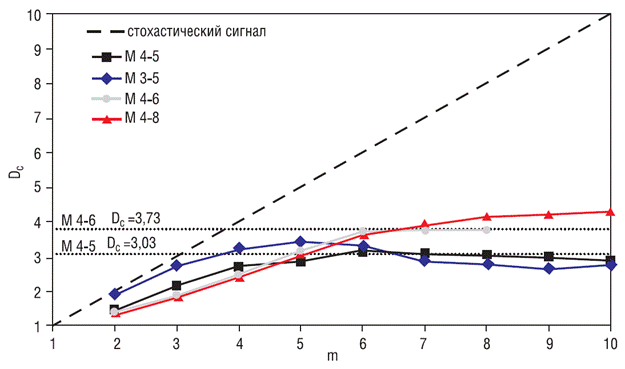
Рисунок 2.30 – График изменения фрактальной размерности 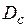от размерности пространства вложения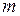

Установлено, что при 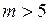наклон линейных участков графиков перестает увеличиваться и зависимость выходит на горизонтальный участок. Таким образом, в данном случае размерность вложения 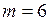, а Dc=3,03. При анализе землетрясений в диапазоне магнитуд от 4 до 6 получено значение 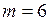, а Dc=3,73. При анализе землетрясений в диапазоне магнитуд от 3 до 5 получено значение 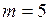, а Dc=2,98.

Из приведенных данных следует вывод, что процесс, приводящий к выделению сейсмической энергии в данном диапазоне магнитуд (от 1 до 8), не является случайным, а зависит от 5-6 основных параметров.

Пример 3. При бурении скважины одной из важнейших технических задач является оценка степени износа долота с целью его своевременной замены. Косвенная оценка состояния бурильного инструмента по изменению механической скорости проходки не всегда надежна, поскольку изменение скорости проходки может быть связано с изменением свойств породы, а не износом долота. Для диагностики состояния долота применена оценка значения корреляционной размерности пульсаций давления промывочной жидкости.

На рисунке 2.31 представлены графики рассчитанных корреляционных размерностей для изношенного и неизношенного инструментов.

Видно, что неизношенное долото характеризуется конечной фрактальной размерностью , в то время как фрактальная размерность изношенного инструмента не ограничивается конечной величиной и определяет случайный процесс, а не детерминированный хаос.

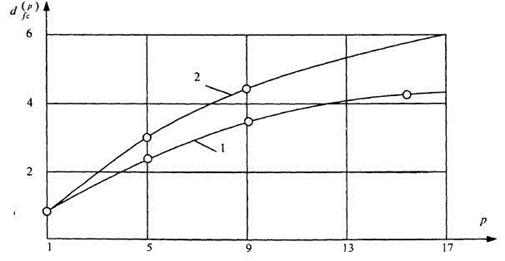
1 – неизношенный инструмент; 2 – изношенный инструмент

Рисунок 2.31 – Кривые Паккарда-Таккенса для выявления хаоса и определения фрактальной размерности

Дата добавления: 2014-01-04