Длина береговой линии

Реально существующие фракталы

Многие береговые линии не имеют естественного масштаба длины. Процессы, формирующие многие из границ раздела между водой и сушей, подобны в широком диапазоне масштабов. На рисунке 2.32 показана часть побережья Норвегии [Федер]. Побережье изрезано большими фьордами, маленькими фьордами и еще более мелкими бухтами и бухточками. Длину этого побережья ни линейкой, ни циркулем измерить не удается. Альтернативный способ измерения длины береговой линии состоит в том, чтобы покрыть карту сеткой, как показано в верхней части рис. 2.32.

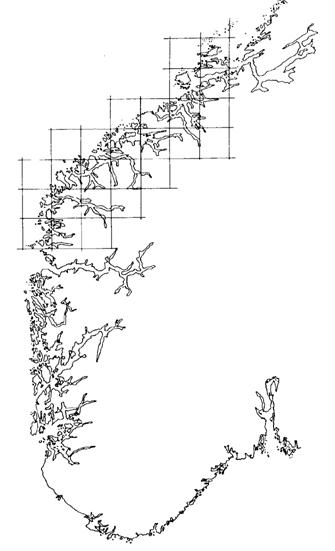
Рисунок 2.32 – Определение фрактальной размерности побережья путем подсчета клеток

Пусть квадратные ячейки сетки имеют размеры 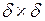. Число 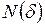таких ячеек, необходимых, чтобы покрыть береговую линию на карте, приближенно равно числу шагов, за которое можно обойти по карте береговую линию циркулем с раствором . Уменьшение приводит к увеличению числа ячеек, необходимых для покрытия береговой линии. Если бы береговая линия Норвегии имела вполне определенную длину 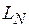, то можно было бы ожидать, что число шагов циркуля или число квадратных ячеек 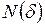, необходимых для покрытия береговой линии на карте, будет обратно пропорционально , а величина 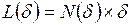при уменьшении будет стремиться к постоянной 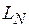. На самом деле это не так.

Как видно из рисунка 2.33, при уменьшении длины шага измеренная длина возрастает. График на этом рисунке выполнен в дважды логарифмическом масштабе и показывает, что при уменьшении измеренная длина береговой линии не стремится к постоянному значению.

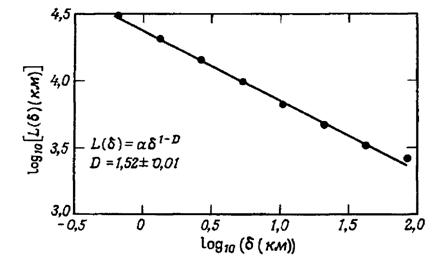
Рисунок 2.33 – График зависимости длины береговой линии 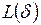от шага измерения в логарифмическом масштабе

График позволяет получить формулу для определения длины береговой линии:

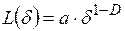. (2.36)

Для обычной кривой можно было бы ожидать, что 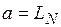(по крайней мере при достаточно малых ) и показатель равен единице. Но для береговой линии Норвегии, как видно из графика, 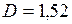. Таким образом, береговая линия – это фрактал с фрактальной размерностью .

По данным Мандельброта фрактальная размерность береговой линии Великобритании составляет .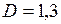

Дата добавления: 2014-01-04