Качественные и количественные признаки хаоса

Прежде всего, следует учесть, что хаотические колебания могут возникнуть в системе, содержащей нелинейный элемент. В линейной системе хаотические колебания отсутствуют.

Существуют следующие качественные признаки, которые могут сигнализировать о возможности появления хаотических компонент:

1) чувствительность к изменению начальных условий;

2) растущая сложность регулярных движений по мере изменения некоторых параметров;

3) фрактальные свойства движения в фазовом пространстве, которые указывают на присутствие странного аттрактора;

4) наличие в непрерывной системе бифуркаций Хопфа;

5) наличие в дискретной системе бифуркаций удвоения периода (логистическое уравнение).

Количественные признаки хаоса определяются ее показателями:

1) положительный показатель Ляпунова;

2) фрактальная размерность аттрактора.

Рассмотрим подробнее каждый из показателей.

Показатель Ляпунова. Хаос в детерминированных системах подразумевает высокую чувствительность к изменению начальных условий. Это означает, что две траектории, близкие друг к другу в фазовом пространстве в некоторый начальный момент, экспоненциально расходятся за малое в среднем время. Если – мера начального расстояния между двумя исходными точками, то, спустя малое время t, расстояние между траекториями, выходящими из этих точек, становится равным:

. (3.20)

Для дискретных систем соответственно имеем

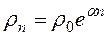. (3.21)

Величина 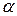называется показателем Ляпунова.

Критерий хаоса в терминах показателя Ляпунова:

При 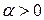– хаотическое движение.

При 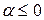– регулярное движение.

Рассмотрим процедуру экспериментального определения показателя Ляпунова.

Вычисление показателя Ляпунова 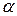начинается с выбора опорной траектории, определения точки на соседней траектории и измерения величины 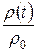, как показано на рисунке 3.10. Далее интегрируются уравнения движения вдоль соседней траектории и определяется ;

Если расстояние становится слишком большим и отклоняется от экспоненциального поведения, нужно найти новую соседнюю траекторию и определить новое начальное расстояние и т.д.;

Показатель Ляпунова находится осреднением:

, (3.22)

где N – число точек на опорной траектории, равное числу соседних траекторий, взятых для получения экспоненциального показателя .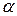

Рисунок 3.10 – Геометрические построения при определении показателя Ляпунова для непрерывных систем

Для дискретных систем:

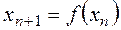(3.23)

показатель Ляпунова характеризует среднюю потерю информации за одну итерацию:

. (3.24)

Пример. Найдем показатель Ляпунова для известного нам логистического уравнения (3.8) при . Используя формулу (3.19):

.

и выражение (3.24), получим:

.

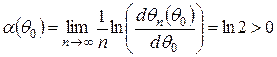Вычисленное значение свидетельствует о том, что при имеет место хаос, в чем мы еще раз убедились.

Дата добавления: 2014-01-04