Основные понятия сопротивления материалов

Введение

При проектировании сооружений и машин инженеру приходится выбирать материал и поперечные размеры для каждого элемента конструкции так, чтобы он вполне надежно, без риска разрушиться или исказить свою форму, сопротивлялся действию внешних сил, передающихся на него от соседних частей конструкции, т. е. чтобы была обеспечена нормальная работа этого элемента. Основания для правильного решения этой задачи дает инженеру наука о сопротивле­нии материалов.

Эта наука изучает поведение различных материалов при действии на них сил и указывает, как подобрать для каждого элемента кон­струкции надлежащий материал и поперечные размеры при условии полной надежности работы и наибольшей дешевизны конструкции.

Иногда сопротивлению материалов приходится решать видоизме­ненную задачу – проверять достаточность размеров уже спроектированной или существующей конструкции.

Требования надежности и наибольшей экономии противоречат друг другу. Первое обычно ведет к увеличению расхода материала, второе же требует снижения этого расхода. Это противоречие является важнейшим элементом научной методики, обусловливающей развитие сопротивления материалов.

Часто наступает момент, когда существующие материалы и ме­тоды проверки прочности не в состоянии удовлетворить потреб­ностям практики, ставящей на очередь решение новых задач (в на­ше время сюда относятся использование больших скоростей в техни­ке вообще, в воздухоплавании в частности, перекрытие больших про­летов, динамические задачи и др.). Тогда начинаются поиски новых материалов, исследование их свойств, улучшение и создание новых методов расчета и проектирования. Прогресс науки о сопротивлении материалов должен поспевать за общим прогрессом техники.

1 Моделирование прочностной надежности элементов
конструкций

Сопротивление материалов – учебная дисциплина, занимающаясярасчетом элементов конструкций на прочность, жесткость и устойчивость, а также изучением механических свойств материалов.

Элемент конструкции – некоторая часть конструкции (сооружения, механизма), предназначенная для расчета.

Прочность - способность тела (детали, элемента конструкции) сопротивляться внешним воздействиям (силовым, температурным и т.д.) без разрушения.

Жесткость – способность тела сопротивляться деформации.

Нагруженная конструкция пребывает в устойчивом равновесии, если она будучи выведенной из него какими-либо причинами, не учитываемыми в расчете, возвращается в первоначальное состояние при устранении указанных причин. В противном случае она не устойчива.

Долговечность состоит в способности конструкции сохранять необходимые для эксплуатации параметры в течение заранее предусмотренного срока времени.

Механические свойства – характеристики материала, описывающие его поведение при внешних силовых воздействиях.

Реальный объект – исследуемый элемент конструкции, взятый с учетом всех своих особенностей: геометрических, физических, механических и других.

Расчетная схема – это реальный объект, у которого отброшены все детали (особенности), не связанные с расчетом, а их влияние заменено силовыми воздействиями.

Основные типы элементов в сопротивлении материалов:

1. Стержень – элемент конструкции, один из размеров которого (длина) много больше двух других.

Рис. 1. Стержень

2. Пластина – элемент конструкции, у которого одно измерение (толщина) мало по сравнению с двумя другими. Пластина, криволинейная до нагружения, называется оболочкой.

Рис. 2. Пластина (а) и оболочка (б)

3. Массивное тело – элемент конструкции, у которого все размеры имеют один порядок.

Материал элементов конструк-ций будем в дальнейшем считать сплошным, однородным и изотропным.

Сплошной материал – материал, не имеющий разрывов, пустот, пор, трещин, включений и т.д.

Однородный материал – материал, в каждой точке которого механические свойства одинаковы и не зависят от величины выделенного объема.

Изотропный материал – материал, свойства которого одинаковы по всем направлениям.

Упругий материал – материал, обладающий способностью восстанавливать первоначальную форму и размеры тела после снятия внешней нагрузки.

Закон Гука: «Перемещения точек упругого тела (в известных пределах нагружения) прямо пропорциональны силам, вызывающим эти перемещения».

Внешние силы – силы взаимодействия между рассматриваемым элементом конструкции и другими телами, связанными с ним.

Классификация внешних сил по способу приложения:

1. Сосредоточенные нагрузки P, M – силы и моменты, площадь действия которых мала по сравнению с размерами объекта (приложены в точке). Единицы измерения , .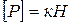

Рис. 4. Внешние силы: а – сосредоточенные силы; б – распределенная нагрузка

2. Распределенная нагрузка q – сила, действующая на некоторой длине стержня. Единица измерения .

Внешние нагрузки различают также по характеру изменения во времени:

· Статические нагрузки медленно и плавно возрастают от нуля до своего конечного значении, а затем остаются неизменными.

· Динамические нагрузки сопровождаются ускорениями как деформированного тела, так и взаимодействующих с ним тел.

· Повторно-переменные нагрузки – силы непрерывно и периодически изменяющиеся во времени.

В сопротивлении материалов не учитывается реальная атомная структура материала твердого тела. Исходя из этого, сплошность и однородность тела обеспечивается не межатомными силами, а гипотетическими внутренними усилиями.

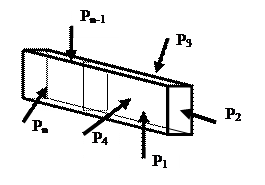
Внутренние усилия – силы взаимодействия (сцепления) между частицами тела, возникающие внутри элемента конструкции, как противодействие внешнему нагружению. Для нахождения величины и направления внутренних усилий мысленно рассекают стержень сечением, перпендикулярным продольной оси стержня, это позволит отбросить ненужный для расчета элемент конструкции (или часть этого элемента), заменить его силой, действие которой будет эквивалентно действию отброшенного элемента (его части) (рис.5). Для определения этой силы нужно использовать уравнения равновесия (уравнения статики)

Уравнения равновесия для определения действия отброшенной части конструкции:

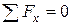
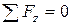(1.1)

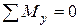
N – осевое (продольное) усилие. Осевое усилие равно сумме проекций всех сил на ось x, действующих с одной стороны сечения: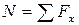

Осевое усилие вызывает растяжение или сжатие элемента.

Q_y, Q_z – поперечные силы. Поперечные силы равны сумме проекций всех внешних сил (с одной стороны сечения) на оси y и z соответственно: ,.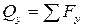

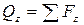Поперечные силы вызывают сдвиг в сечении элемента.

М_x – крутящий момент (М_кр). Крутящий момент равен сумме моментов внешних сил (с одной стороны сечения) относительно оси x: .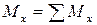

Крутящий момент вызывает кручение элемента.

М_z, М_y – изгибающие моменты. Изгибающие моменты равны сумме моментов внешних сил относительно осей y и z соответственно: , .

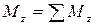Изгибающие моменты вызывают изгиб элемента.

Таким образом, введя понятие внутренних усилий можно свести все многообразие внешних нагрузок к 6-ти силовым факторам и представить даже самое сложное внешнее воздействие как сочетание 4-х видов сопротивления: растяжение-сжатие, сдвиг, кручение, изгиб.

Чтобы характеризовать закон распределения внутренних сил по сечению, необходимо ввести для них числовую меру. За такую меру принимается напряжение.

Рассмотрим сечение F некоторого тела (рис.1.6), в котором выделим элементарную площадку dF, в пределах которой выделена внутренняя сила dR. За среднее напряжение на площадке принимаем отношение

. (1.2)

Будем уменьшать площадку dF, стягивая ее в точку. Поскольку среда непрерывна, возможен предельный переход при 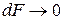. В пределе получаем

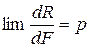. (1.3)

Векторная величина р представляет собой полное напряжение в точке. Напряжение имеет размерность кН/м².

Полное напряжение р может быть разложено на три составляющие: по нормали, к плоскости сечения и по двум осям в плоскости сечения (рис.6). Проекция полного напряжения на нормаль к сечению обозначается 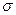и называется нормальным напряжением. Составляющие в плоскости сечения называются касательными напряжениями и обозначаются .

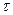Дата добавления: 2014-01-04