Пример исследования бифуркационного поведения летательного аппарата

Рассмотрим поведение симметричного реактивного летательного аппарата, для которого потеря устойчивости соответствует одной элементарной катастрофе.

Переменные состояния 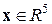: три компоненты угловой скорости 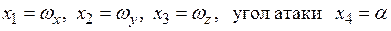, угол скольжения .

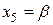Управляющие параметры 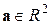(мы их обозначим так, как принято в теории управления – через 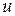и назовем управлением:

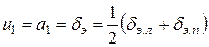, (4.38)

где 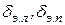– отклонение левого и правого элеронов, соответственно;

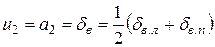, (4.39)

где 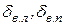– отклонение левого и правого рулей высоты, соответственно.

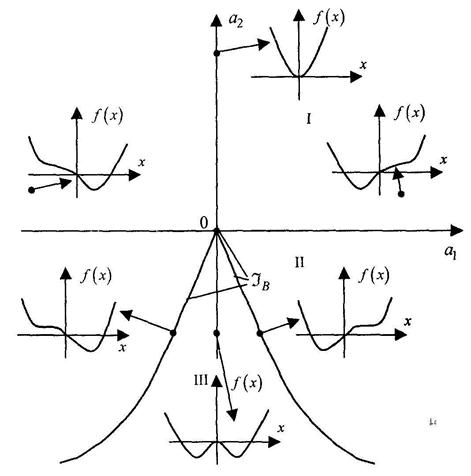
I – одна критическая точка; II – две критические точки; III – три критические точки

Рисунок 4.9 – Бифуркационное множество J_B и вид функции при разных значениях параметров

Таким образом, имеем: .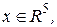

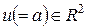Уравнения движения летательного аппарата имеют следующий вид:

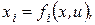
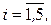
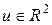, (4.40)

а стационарное решение:

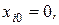
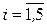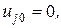
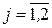, . (4.41)

Разложив систему уравнений (4.40) в ряд Тейлора, а также произведя необходимые преобразования для выделения аэродинамических и управляющих составляющих, получим матричное представление, где каждому параметру состояния соответствует пара совместных уравнений для управлений 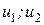. Решение этих уравнений единственно при условии, что определитель системы не равен нулю.

Параметрическое представление кривых складки 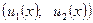показано на рисунке 4.10. Эта проекция многообразия катастрофы на плоскость управляющих параметров (управлений) 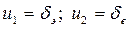формирует бифуркационное множество J_B. Множество J_B делит плоскость R² управляющих параметров на открытые непересекающиеся области, в которых функция Ф(х; u) имеет различное число (1, 3, 5) критических точек, а динамическая система, соответственно, 1, 3, 5 устойчивых или неустойчивых состояний равновесия.

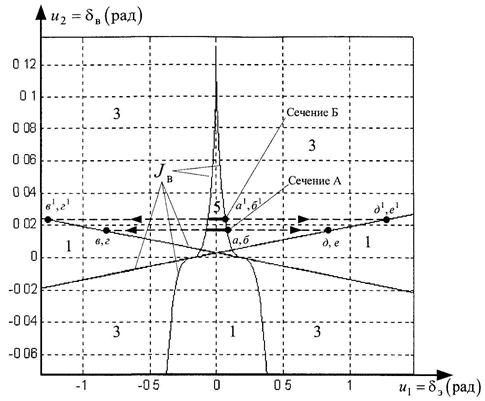
Рисунок 4.10 – Бифуркационное множество J_B многообразия катастрофы реактивного летательного аппарата в плоскости управляющих параметров 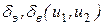. Цифры указывают на число состояний равновесия (устойчивых и неустойчивых)

Рассмотрим случай, когда управление производится только элеронами 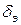, то есть 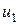при фиксированном положении руля высоты и₂ =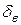= 0,01 рад~0,6° (сечение А, рис. 4.10).

Пусть 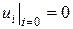и мы начинаем медленно увеличивать угол 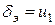. Сначала переменная 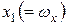линейно реагирует на изменение 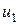(рис. 4.11), но при достижении точки а (~6˚), то есть при попадании на бифуркационное множество J_B скачком переходит вниз (с точки а на точку б, рис. 4.11).

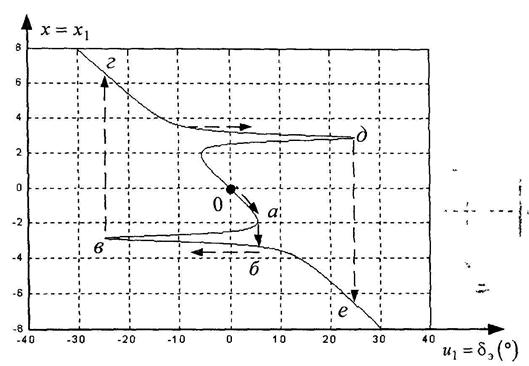
Рисунок 4.11 – Зависимость координаты 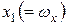от угла поворота элеронов при постоянном отклонение руля высоты 0,6° (сечение А)

На этом листе состояние летательного аппарата по координате 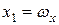совершенно неуправляемо при отклонении элеронов 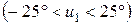. Другими словами, если пилот попытается вернуть летательный аппарат в состояние х = 0, уменьшая 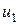при и₂ = const, он потерпит неудачу. Летательный аппарат не будет реагировать на изменение 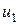до тех пор, пока не достигнет значения 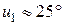(точка в, рис. 4.11), при котором происходит скачкообразный переход на верхний лист.

Последующее увеличение 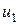вновь сопровождается отсутствием необходимой реакции вплоть до значения 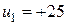(точка д), при котором точка х вновь перескочит на нижний лист (точка е). Средний лист остается недостижимым при и₂ = const = 0,6°. Заставить систему вернуться на средний лист (в том числе в состояние х = х ₁ = 0) можно только изменив оба управления 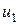и .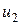

Если взять другое сечение, и₂ = const, например, увеличить и₂ до и₂ =1,2° (сечение Б, рис. 4.10), то точки скачкообразного перехода с нижнего листа на верхний и наоборот еще более сдвинутся (точка г'~ – 60°).

Таким образом, на основе использования теории катастроф возможно качественное изучение особенностей поведения динамических управляющих систем, в том числе получение бифуркационных множеств и устойчивых компонент многообразия систем.

Литература

1. Методы классической и современной теории автоматического управления: Учебник в 3-х т. Т.3: Методы современной теории автоматического управления / Под ред. Н. Д. Егупова. – М.: Изд-во МГТУ им. Н. Э. Баумана. 2000. – 748 с.

2. Чуличков А. И. Математические модели нелинейной динамики. – М.: ­ФИЗМАЛИТ, 2000. – 296 с.

3. Кроновер Р. М. Фракталы и хаос в динамических системах. Основы теории. Москва: Постмаркет, 2000. – 352 с.

4. Морозов А. Д. Введение в теорию фракталов. – Москва-Ижевск: Институт компьютерных исследований, 2002. – 160 с.

5. Федер Е. Фракталы: Пер. с англ. – М.: Мир, 1991. – 254 с.

6. Пригожин И., Стенгерс И. Порядок из хаоса: Новый диалог человека с природой: Пер. с англ. / Общ. ред. В.И. Аршинова, Ю.Л. Климентовича и Ю.В. Сачкова. – М.: Прогресс, 1986. – 432 с.

7. Арнольд В. И. Теория катастроф. – М.: Наука, 1990. – 126 с.

8. Детерминированный хаос. [Электронный ресурс]. Режим доступа: http://www.vevivi.ru/best/Determinirovannyi-khaos-ref54258.html

9. Захаров В.С. Анализ корреляционной размерности временных рядов выделения сейсмической энергии. [Электронный ресурс]. Режим доступа: http://dynamo.geol.msu.ru/personal/vsz/papers/Dubna_07.pdf

Дата добавления: 2014-01-04