Нерациональное поведение

Психологи и экономисты обнаружили ряд парадоксов, показывающих, что поведение человека отличается от рационального. Экспериментальным путем обнаружен ряд принципов (эвристик), на которые опирается человек при принятии решения. Наиболее важные из них следующие:

1) Суждение по представительности. Человек судит о том, что предмет А (или событие) относится к классу В лишь на основании сходства по какому-либо параметру с типичным представителем класса В, но не на основании всего комплекса параметров. При этом также игнорируются вероятности отнесения к тому или иному классу и размер выборки.

2) Суждение по встречаемости и субъективной важности. Люди часто определяют вероятность событий по тому, как часто они сами сталкивались с этими событиями и насколько важными для них были эти встречи.

3) Суждение по точке отсчета. Если при определении вероятностей используется начальная информация как точка отсчета, то она существенно влияет на результаты. Например, человек лишь частично исправит завышенные или заниженные начальные значения.

4) Сверхдоверие. Люди склонны переоценивать свои суждения, например, о вероятности редких событий.

5) Стремление к исключению риска. Многочисленные работы показывают, что как в экспериментах, так и в реальных ситуациях, люди стремятся избежать развития событий, связанного с риском. Они выбирают средние и хуже средних альтернативы, только, чтобы не возникли ситуации, где хотя бы при очень малых вероятностях возможны большие потери.

Насколько важен учет нерационального поведения человека при объяснении и моделировании ситуаций? Это зависит от задач, которые стоят перед объясняющим. Например, если мы рассматриваем уже прошедшие события, например, насколько раскупается тот или иной товар, то нам неважно, на основании каких побуждений этот товар раскупается. Здесь важна цифры типа, какой процент населения покупает данный товар и т.п.

Если же мы хотим предсказать будущие события (как будет раскупаться товар), то здесь мы уже должны знать, чем руководствуется человек при его покупке, в том числе и нерациональные с точки зрения теории рационального выбора мотивы.

7. Понятие о многокритериальности в принятии решений

В середине прошлого столетия для решения военных, производственных и социально-экономических задач широкое распространение получили методы исследования операций. Основными этапами решения любой задачи в исследовании операций являются:

а) построение модели;

б) выбор критерия оптимальности;

в) нахождение оптимального решения.

Для этого подхода характерны следующие особенности.

1) Предполагается, что модель, правильно отражающая действительность, при данном критерии оптимальности приводит к единственному решению.

2) По заказу руководителя аналитики исследуют организацию, внешнюю среду и строят адекватную модель. В этой работе сам ЛПР чаще всего не нужен, аналитики самостоятельно находят удачное решение.

3) Существует объективный и единственный критерий успехов в применении методов исследования операций. Если проблема, требующая решения, ясна и критерий определен, то аналитический метод однозначно показывает, насколько новое решение лучше старого.

Примеры задач этого типа: обобщенная транспортная задача (оптимизация множества маршрутов), задача о назначениях - поручение работы при выполнении сложной задачи и т.д.

Методы исследования операций работают хорошо, когда имеется единственный критерий. Когда же критериев несколько, ситуация существенно изменяется. Например, в случае обобщенной транспортной задачи. Пусть некая авиакомпания хочет минимизировать издержки при условии максимума прибыли и максимума удобств для пассажиров. Как согласовать эти критерии? В рамках самой задачи невозможно найти оптимальное решение, для уточнения соотношений между критериями необходима дополнительная информация о возможных соотношениях этих критериев, и эта информация может быть получена только от ЛПР этой компании.

Вообще многокритериальные задачи, возникшие в идеологии методов исследования операций, имеют одну общую особенность: модель, описывающая множество допустимых решений, объективна, но качество решения оценивается по многим критериям. Для выбора наилучшего варианта решения необходим компромисс между оценками по различным критериям. В условиях задачи отсутствует информация, позволяющая найти такой компромисс, т.е., невозможно аналитическим путем найти соотношение между критериями.

8. Общая постановка многокритериальной задачи

Рассмотрим постановку решения классической задачи при двух критериях, когда в качестве критериев используются стоимость и эффективность какого-либо проекта, например, системы противоракетной обороны, транспортной системы города и т.п.

Такого рода модели состоят из двух частей: модели стоимости и модели эффективности. Например, для системы противоракетной обороны модель стоимости представляет зависимость общей стоимости проекта от количества ракет (линейная зависимость), а модель эффективности – зависимость вероятности поражения от количества ракет (нелинейная зависимость, выходит на насыщение). Обе модели можно рассматривать как объективные: они строятся на базе фактических данных, надежного статистического материала. Однако выходные параметры этих моделей не могут быть объединены аналитически, для этого необходимо суждение руководителя, который определяет значения стоимости и эффективности.

Существует несколько эвристических приемов, позволяющих сделать более обоснованный вывод в такой ситуации.

В первом случае мы (ЛПР) задает предельно допустимые значения для всех критериев, кроме одного, по которому и проводится оптимизация. Например, в случае пары критериев «эффективность-стоимость» ЛПР задает предельное значение стоимости, и в этом случае стоимость из разряда критериев переходит в разряд ограничений. Решение ищется для эффективности при учете ограничений на стоимость. Как правило, такой метод (перевод части критериев в ограничения) возможен лишь при небольшом количестве критериев, четко и однозначно описывающих ситуацию.

В более сложных случаях (большое количество критериев, неясные последствия и т.д.) в качестве предварительного шага для выбора соотношения критериев используется метод построения множества Эджворда-Парето (или просто множества Парето). Это множество представляет собой область максимально возможных значений параметров, включая различные соотношения между параметрами.

Например, для задачи «эффективность-стоимость» множество Эдворда-Парето может быть представлено в виде следующей зависимости (рис.2.):

В данном случае линия на графике представляет собой множество Эдворда-Парето, являющееся, по сути, различными вариантами соотношений между критериями оптимальности задачи. Любое из перечня оптимальных решений лежит на этой линии и задача ЛПР состоит в том, чтобы выбрать некоторую точку на этой линии.

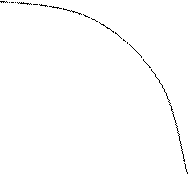
Эффективность

max

min

max min Стоимость

Рис.2..2 Представление задачи при двух критериях

В случае большего количества критериев линия превращается в многомерную область Парето, но и в этом случае сохраняется ее основное свойство – обозначать область наиболее эффективных решений. Таким образом, максимум, на что способны классические методы исследования операций – это нахождение области Парето, а уже в пределах этой области решение должен выбирать ЛПР. Вообще говоря, это тоже очень непростая задача, в связи с чем разработан ряд методов для увеличения обоснованности принятого решения.

9. Методы поиска решений в многокритериальных задачах

Разработано множество методов согласования критериев в многокритериальных задачах. Их можно разделить на несколько больших групп:

1) Метод весовых коэффициентов важности критериев. Этот подход основан на получении дополнительной информации от ЛПР и приданием на основе этой информации численных значений важности критериев. Задача при этом сводится к объединению многих критериев в один глобальный критерий, вычисляемый по формуле:

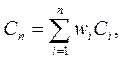(19.2),

где C_i – частные критерии (i= 1,…,N); w_i – веса (коэффициенты важности критериев, их сумма равна единице.

2) Метод представления решения многокритериальной задачи в виде векторов. В основе этого метода лежит предположение, что ЛПР может непосредственно сравнивать решения, предъявляемые ему в виде векторов в критериальном пространстве, и систематически искать в этом пространстве наилучший вектор. Одной из наиболее известных разновидностей этого метода является компьютерное представление на экране дисплея в виде различных попарных сочетаний критерий, и выбора наилучшего сочетания критериев путем их последовательного попарного сравнения.

3) Методы дальнейшего исследования предпочтений ЛПР и расчет их наилучшего сочетания той или иной методики, например, с помощью метода анализа иерархий. Эту группу методов мы рассмотрим подробнее в последующих лекциях

Литература к теме:

1. Ларичев О.И. Теория и методы принятия решений – М.: Логос –

2000. – 296 с.

2. Саати Т., Кернс К. Аналитическое планирование. Организация систем – М.: Радио и связь – 1991. – 224 с.

Дата добавления: 2014-01-03