
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Сферы, шара, цилиндра
|
|
|
|
Лекция 2. Применения теоремы Гаусса для расчета
электростатических полей заряженных плоскости,
Теорема Гаусса легко обобщается для случаев непрерывного распределения заряда: в пространстве с объемной плотностью r=dq/dV, с поверхностной плотностью s= dq/dS, по линии с линейной плотностью l=dq/dl. При этом суммирование в формуле (10) заменится интегрированием: для заряда, распределенного
по объему 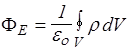 ; (11)
; (11)
поверхности 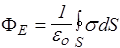 ; (12)
; (12)
линии 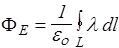 . (13)
. (13)
Использование теоремы Гаусса в рассматриваемых ниже примерах, упрощает вычисление напряженности. Для краткости будем называть гауссовой ту (воображаемую, а не заряженную!) замкнутую поверхность S, по которой ведется интегрирование при вычислении потока.
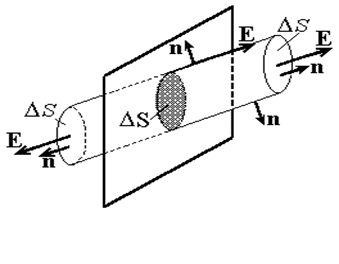
|
| Рис.6 |

|
Поле заряженной плоскости. Пусть бесконечная плоскость равномерно заряжена положительно с плотностью заряда s. Вектор Е должен быть везде направлен перпендикулярно плоскости в обе стороны от нее. В противном случае составляющая вектора Е вдоль плоскости заставила бы заряды переместиться, что противоречит равномерности распределения заряда. Очевидно, вектор Е одинаков по модулю для всех равноудаленных от плоскости точек. Поэтому в качестве гауссовой поверхности логично выбрать прямой цилиндр, симметричный относительно плоскости, как показано на рис. 6. Поток вектора Е через боковую поверхность этого цилиндра равен нулю, так как (Е,n)=0 вследствие перпендикулярности векторов n и Е. Поэтому полный поток равен 2 ЕDS, где DS - площадь каждого торца. Внутри цилиндра заключен заряд sDS (показан штриховкой). По теореме Гаусса 2 ЕDS = sDS. Следовательно,
Е= s/2eо. (14)
| Рис.7 |
Поле двух заряженных плоскостей. Пусть две бесконечные равномерно заряженные плоскости (с плотностями зарядов s и -s) расположены параллельно на расстоянии d друг от друга (рис.7). Сложим векторно напряженности, создаваемые каждой плоскостью. Поле справа и слева от плоскостей равно нулю (Е=s/2 eo -s/2 eo =0), а между ними - (Е=s/2 eo +s/2 eo), следовательно,
Е=s/eo. (15)
Такое поле создается в плоском конденсаторе (за исключением области краев). Если плоскости заряжены одноименно, то поле между ними равно нулю, а снаружи Е=s/eo.

|
| Рис.8 |
Поле заряженного бесконечного цилиндра. Пусть поверхность бесконечно длинного цилиндра радиуса R заряжена равномерно и положительно так, что на единицу его длины приходится заряд l. Очевидно, вектор Е должен быть перпендикулярен оси цилиндра и его модуль может зависеть только от расстояния r от оси. Гауссову поверхность нужно взять в виде прямого цилиндра высотой h, расположенного коаксиально с заряженным (рис.8). Поток вектора Е через боковую поверхность гауссова цилиндра равен Е2prh (вектор Е направлен по нормали к боковой поверхности), а через торцы - нулю, так как вектор нормали к торцам перпендикулярен Е. Для r > R имеем: Е2prh=lh/eo, следовательно,
 (r>R). (16)
(r>R). (16)
Если R ¹0, то при r ® R, Е=l/peoR, т.е. на поверхности Е стремится к конечному пределу. При r < R заряд внутри гауссова цилиндра отсутствует, следовательно Е×2prh= 0, поэтому напряженность внутри цилиндра равна нулю. При R ®0, Е ®¥. Это значит, что вблизи тонкого острия можно создавать поля исключительно высокой напряженности. Вследствие этого заряды могут легко покидать острие, сохраняя информацию о расположении атомов “своего” вещества. На подобном принципе основано устройство ионного микроскопа, позволившего впервые “увидеть” атомы.
Формула (16) описывает также поле бесконечной равномерно заряженной с линейной плотностью l нити. Гауссова поверхность и рассуждения аналогичны приведенным для поля вне заряженного цилиндра.
|
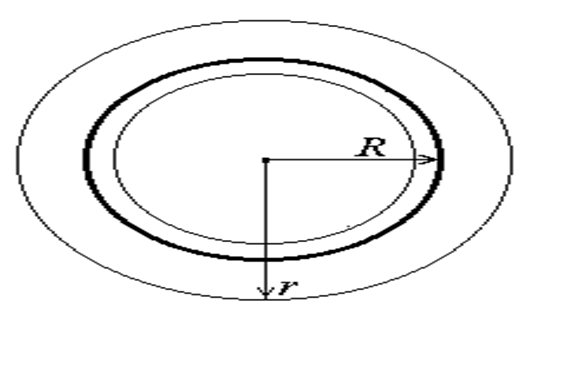
Поле заряженной сферы. Пусть сфера радиуса R равномерно заряжена c поверхностной плотностью s>0. Вследствие центральной симметрии, вектор Е направлен вдоль радиуса от центра, и его модуль зависит только от расстояния r от центра. Выберем в качестве гауссовой поверхности концентрическую с заряженной сферу радиуса r>R (рис.9). По теореме Гаусса поток вектора Е через эту сферу равен Е4pr2=s4pR2/eo, следовательно, поле вне сферы подобно полю точечного заряда
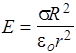 , (r³R). (17)
, (r³R). (17)
На заряженной поверхности сферы Е=s/eo. При r<R заряд внутри гауссовой поверхности равен нулю (Е4pr2= 0), поэтому напряженность равна нулю.
| Рис.9 |
Поле заряженного по объему шара. Пусть шар радиуса R равномерно заряжен по объему с плотностью заряда r. Гауссову поверхность выбирают также, как в случае заряженной сферы (рис.9).
|
При r>R, следуя теореме Гаусса, получаем Е4pr2=4pr R3/3eo, откуда
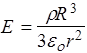 , (r³R). (18)
, (r³R). (18)
При r<R внутрь гауссовой сферы попадает часть заряда шара, поэтому Е4pr2=4prr3/3eo, Þ
| Рис.10 |
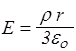 . (19)
. (19)
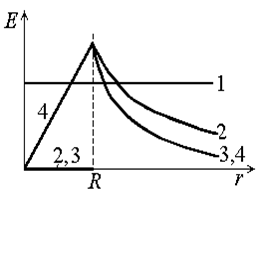
На рис.10 представлены графики зависимости Е от r для равномерно заряженных: плоскости (1), цилиндра (2), сферы (3), шара (4).
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 961; Нарушение авторских прав?; Мы поможем в написании вашей работы!