И потенциала. Поле диполя

Электрического поля. Потенциал. Связь напряженности

Лекция 3. Теорема о циркуляции вектора напряженности

Как известно из курса механики, работа сил центрального поля зависит только от начального и конечного положений частицы. Поэтому работа поля по перемещению частицы вдоль замкнутой траектории равна нулю. Такие поля называются потенциальными.

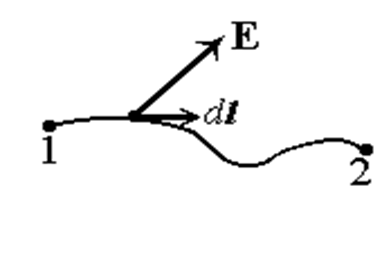
Рис.11

Вычислим работу сил электростатического поля, совершаемую при перемещении точечного заряда q из точки 1 в точку 2 (рис.11)

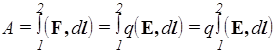, а затем разделим обе части на q.

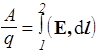. (20)

Отношение А/q численно равно работе поля по переносу единичного заряда из точки 1 в точку 2. Интеграл вида (20), вычисленный вдоль замкнутого контура, называется циркуляцией и обозначается .

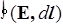Теорема о циркуляции вектора Е. Циркуляция вектора напряженности электростатического поля по любому замкнутому контуру равна нулю: 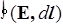=0.

Доказательство. Электростатическое поле точечного заряда является центральным и, следовательно, потенциальным. Поэтому работа его сил на замкнутом пути равна нулю:

,

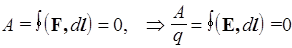Таким образом, и циркуляция вектора Е поля точечного заряда равна нулю. Докажем это для поля системы из n зарядов. Так как напряженность Е поля системы равна сумме напряженностей, создаваемых каждым зарядом в отдельности,

Е = Е ₁ + Е ₂ + Е ₃ + ... + Е _n.

Умножим это равенство скалярно на вектор перемещения d l вдоль произвольного замкнутого контура и проинтегрируем по этому контуру:

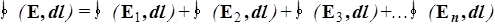. (21)

Каждый интеграл в правой части равен нулю как циркуляция вектора напряженности поля соответствующего точечного заряда, следовательно, и вся сумма равна нулю. Таким образом, циркуляция вектора напряженности системы точечных зарядов равна нулю.

Переходя к пределу в выражении (21), нетрудно убедиться, что и для непрерывно распределенного заряда циркуляция вектора Е равна нулю.

Потенциал. Из независимости от траектории интеграла 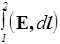следует, что его можно однозначно представить в виде разности значений некоторой функции координат j на нижнем и верхнем пределах

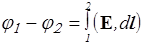, (22)

или

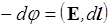. (23)

Введенная таким образом функция j( r ) называется потенциалом. Разность потенциалов j₁ - j₂ численно равна работе сил поля по переносу единичного положительного заряда из точки 1 в точку 2. Из того, что поле способно совершить такую работу, следует, что в точках 1 и 2 заряд обладает различной потенциальной энергией. Поэтому потенциал можно также определить как потенциальную энергию пробного заряда q в поле, отнесенную к его величине

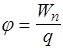. (24)

Таким образом потенциал определен с точностью до произвольной константы.

Рис.12

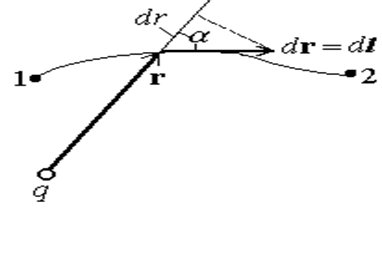
Потенциал поля точечного заряда. Поскольку заряд q (рис.12) создает поле с напряженностью Е= q e _r/4 pe_or², скалярное произведение в формуле (23) можно преобразовать

,

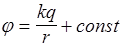где k =1/4 pe_o, и учтено, что dl×cosa = dr (так как dr - это проекция перемещения d l на направление радиус-вектора r). Обычно полагают потенциал при r®¥ равным нулю. Тогда const =0 и потенциал поля точечного заряда равен

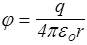. (25)

Если заряды распределены непрерывно с объемной плотностью r (r), то точечным следует считать заряд dq = rdV. Тогда потенциал представляется интегралом по объему

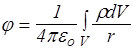. (26)

Аналогично, если заряды распределены по поверхности или линии, то интегрируют по поверхности или линии соответственно

.

Единицей измерения потенциала является вольт [ B ] - потенциал точки, для удаления из которой положительного заряда в 1 Кл на бесконечность электрическое поле совершает работу в 1 Дж.

Связь напряженности и потенциала. Пусть d l - вектор малого перемещения вдоль траектории. Это значит, что радиус-вектор r (x,y,z)получил приращение d l (dx,dy,dz). Тогда скалярное произведение (Е, d l) равно

(Е, d l) = E_xdx + E_ydy+ E_zdz.

Кроме того, (Е, d l)=- dj, поэтому E_x= -¶ j/ ¶ x, E_y=- ¶ j/ ¶ y, E_z =-¶ j/ ¶ z. Пусть i, j, k - орты декартовой системы координат.

Тогда

Е = i E_x + j E_y+ k E_z,

или

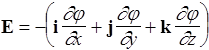. (27)

Дифференциальную операцию в круглых скобках, примененную к скалярной функции j, называют градиентом этой функции (grad j). Следовательно, связь напряженности и потенциала можно выразить так

Е = - grad j. (28)

Пусть требуется найти E_l - проекцию вектора Е на направление некоторого вектора l. Так как (Е, d l) = E_l × dl и (Е, d l)= - dj, то

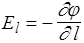. (29)

Эквипотенциальные поверхности. Так называются поверхности в пространстве, на которых потенциал имеет постоянное значение. Чтобы показать, что вектор Е направлен перпендикулярно эквипотенциальной поверхности, спроектируем его на касательное к этой поверхности направление, характеризуемое вектором l. Поскольку величина потенциала постоянна на эквипотенциальной поверхности, производная ¶ j/ ¶ l равна нулю, а с учетом (29), равна нулю и проекция E_l. Если в некоторой точке поверхности проекция вектора на любое касательное направление равна нулю, он перпендикулярен этой поверхности. Таким образом, вектор Е перпендикулярен эквипотенциальной поверхности и направлен с учетом знака в сторону максимальной скорости убывания потенциала.

Потенциал системы зарядов. Запишем выражение напряженности поля системы из n зарядов

Е = Е ₁ + Е ₂ + Е ₃ + ... + Е _n.

Умножим обе части этого равенства скалярно на d l

(Е, d l) = ((Е ₁ + Е ₂ + Е ₃ + ... + Е _n ), d l) = - dj₁ - dj₂ - dj₃... - dj_n = - dj.

Проинтегрируем это равенство, учитывая, что в знаменателе выражения (25) стоит расстояние от заряда до точки с радиус-вектором r, где вычисляется потенциал. В данном случае это расстояние равно | r _i - r | для каждого из n точечных зарядов. Следовательно, потенциал поля системы зарядов равен

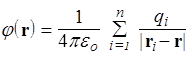. (30)

Итак, потенциал электростатического поля системы точечных зарядов равен алгебраической сумме потенциалов, создаваемых каждым из зарядов, независимо от других. Чтобы получить потенциальную энергию W_п заряда q в поле системы зарядов { q_i }, достаточно умножить потенциал j (r) на q

.

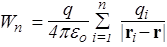Потенциальная энергия измеряется работой поля системы зарядов по переносу заряда q из точки (с радиус-вектором r) на бесконечность.

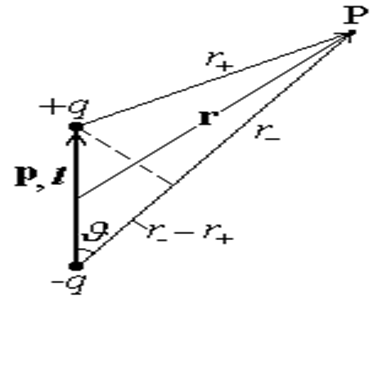
Поле диполя. Диполь - это система из двух равных разноименных зарядов, расположенных друг от друга на расстоянии l << r, где r - радиус-вектор некоторой точки Р поля относительно центра диполя (рис.13). Введем вектор дипольного момента р =q l. Потенциал в точке Р вычислим, как алгебраическую сумму потенциалов зарядов диполя

.

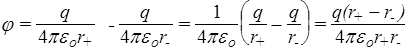Так как l<< r, положим, что r₊×r_-» r², а (r₊- r_-)» lcosJ. Тогда

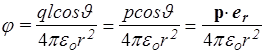. (31)

Рис.13

Вычислим проекции вектора Е на вектор r (E_r) и перпендикулярное ему направление (E_J)

.

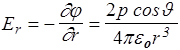Поскольку в перпендикулярном к r направлении дифференциально малое приращение координаты равно rdJ, то

.

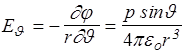Модуль вектора напряженности равен

,

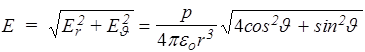что после подстановки sin²J+cos²J =1 дает

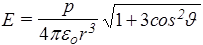. (32)

Напряженность поля диполя убывает обратно пропорционально третьей степени расстояния - быстрее, чем поле точечного заряда. Из формулы (32) легко получить параллельную (J= 0) и перпендикулярную оси диполя (J= p/2) составляющие вектора Е

,

Дата добавления: 2014-01-04