Закон Джоуля-Ленца

Лекция 4. Постоянный электрический ток. Закон Ома.

Ток в проводнике возникает вследствие движения заряженных частиц. Сила тока равна производной по времени от суммарного заряда Q (t), прошедшего через поперечное сечение проводника к моменту времени t:

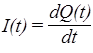(33)

Средней по сечению проводника плотностью тока называется отношение силы тока к площади сечения проводника:

.

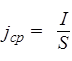Вектор плотности тока. В общем случае плотность тока может быть разной в различных точках сечения. Величина вектора плотности тока численно равна заряду, протекающему в единицу времени через дифференциально малую площадку, расположенную перпендикулярно скорости направленного движения зарядов. Если в проводнике заряженные частицы имеют концентрацию n, заряд е и среднюю скорость v _ср, то вектор плотности тока j равен

j = en v _ср, (34)

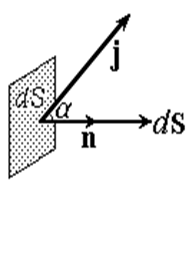
и имеет направление вектора v _ср. Выделим внутри проводника малую площадку dS (рис.14). Заряд, прошедший через нее за время dt, равен

,

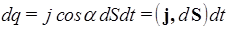Рис.14

где a - угол между j и нормалью n к элементу поверхности dS, d S - вектор, имеющий величину dS и направление n. Заряд dQ, прошедший за время dt через все поперечное сечение проводника равен интегралу

.

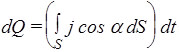Откуда ток, протекающий через все сечение S проводника равен 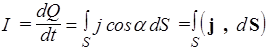. Следовательно,

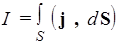. (35)

Таким образом, сила тока является потоком вектора плотности тока. Единица силы тока - ампер [ A ].

Электродвижущая сила (эдс). Если проводник внести в электростатическое поле, то заряды будут двигаться до тех пор, пока поле этих зарядов не скомпенсирует внешнее поле, после чего ток прекратится (практически мгновенно). Для поддержания тока к зарядам необходимо приложить силы не электростатической природы, называемые сторонними. Пусть на некотором участке цепи действуют сторонние силы, напряженность поля которых Е^*, и электростатическое поле с напряженностью Е. Вычислим работу, необходимую для переноса заряда q из некоторой точки 1 в точку 2

.

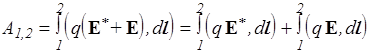Разделим обе части на q

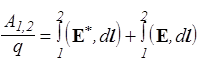. (36)

Отношение А_1,2/q называется напряжением U и представляет собой работу полей сторонних сил и сил электростатического поля по перемещению единичного положительного заряда из точки 1 в точку 2. Второе слагаемое - это введенная ранее разность потенциалов j₁-j₂ (см. формулу (22)), а первое называется электродвижущей силой (эдс). Таким образом, эдс численно равна работе поля сторонних сил, необходимой для переноса единичного положительного заряда из точки 1 в точку 2

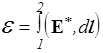. (37)

Если точки 1 и 2 совпадают - цепь замкнута - и эдс представляет собой циркуляцию вектора напряженности поля сторонних сил. Таким образом,

U=e +(j₁-j₂). (38)

Участок цепи, на котором не действуют сторонние силы (e =0) называется однородным и для него U=j₁-j₂. Таким образом, для однородного участка цепи напряжение совпадает с разностью потенциалов на его концах.

Закон Ома в дифференциальной форме. Найдем связь между векторами j и Е, пользуясь не строгими физическими соображениями. Пусть электрон движется в поле с напряженностью Е. Тогда, в соответствии со вторым законом Ньютона, он приобретает ускорение a =- e E /m и его скорость возрастает по закону

v= v _о+ a t = v _о-,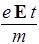

где v _о - скорость электрона в отсутствии внешнего поля. При каждом соударении происходит передача кинетической энергии электрона решетке, и скорость падает почти до нуля. Допустим, что увеличение скорости происходит в течение среднего времени между столкновениями t. Усредним последнее выражение

.

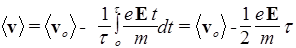Но < v _o>=0 вследствие хаотичности скорости в отсутствии поля. Поэтому

.

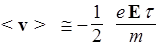Теперь, учитывая (34), вычислим плотность тока

.

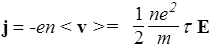Поскольку произведение постоянных величин, стоящих перед вектором Е, представляет собой также некоторую константу, плотность тока в каждой точке проводника пропорциональна напряженности поля в этой точке. Обычно этот результат выражают в виде

j = s E, (39)

называемом законом Ома в дифференциальной форме: плотность тока в каждой точке проводника пропорциональна напряженности поля в этой точке. Коэффициент пропорциональности s называется проводимостью. Закон Ома с высокой точностью выполняется только для металлов. Для других проводящих сред зависимость может быть более сложной.

Часто закон Ома в дифференциальной форме записывают в виде

,

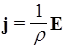где r - удельное сопротивление проводника. Удельное сопротивление металлов линейно возрастает с увеличением температуры t,^оС:

r = r_o (1+ at),

где a - температурный коэффициент сопротивления; r и a - табличные величины.

Дата добавления: 2014-01-04