Сила Лоренца. Закон Био-Савара-Лапласа

Закон Ома в интегральной форме. В простейшей форме этот закон сначала был установлен экспериментально: величина тока, протекающего по металлическому проводнику, прямо пропорциональна напряжению на его концах

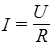. (40)

Величина R называется сопротивлением проводника и зависит от его формы, температуры и материала

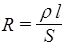, (41)

где l - длина проводника, S - площадь его поперечного сечения. Единицей измерения величины R является [ Ом ], размерность удельного сопротивления r - [ Ом×м ].

Закон Ома в интегральной форме нетрудно вывести, исходя из дифференциальной формы. Возьмем для простоты проводник в виде прямого цилиндра сечения S, и пусть плотность тока во всех точках одного и того же сечения одинакова и постоянна. Тогда

.

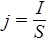Подставим эту величину в выражение закона Ома в дифференциальной форме (rj=E) и проинтегрируем в пределах длины проводника

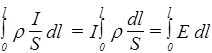= U, (42)

где мы вынесли величину I, так как ток предположен постоянным. Интеграл 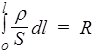есть электрическое сопротивление проводника и определяется его геометрией и удельным сопротивлением. Если r и S постоянны по всей длине проводника, то 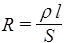, и выражение (42) переходит в (40), что и требовалось показать.

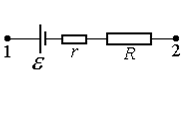
Рис.15

Рассмотрим неоднородный участок цепи. Очевидно, можно считать реальный источник эдс эквивалентным идеальному, к которому последовательно подсоединено (внутреннее) сопротивление r (рис.15). Тогда закон Ома в интегральной форме следует сформулировать так: произведение силы тока в проводнике и его сопротивления равно сумме разности потенциалов на концах проводника и действующей в проводнике эдс

I(R+r)= (j₁-j₂)+ e. (43).

В замкнутой цепи точки 1 и 2 совпадают, поэтому (j₁-j₂) = 0, и закон Ома принимает вид

.

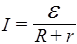Когда цепь разомкнута, ток в ней равен нулю, тогда e= | j₁-j₂|: эдс источника равна разности потенциалов на его зажимах при разомкнутой цепи.

Закон Джоуля-Ленца. Работа, совершаемая при перемещении заряда q из точки 1 в точку 2 участка цепи, равна

.

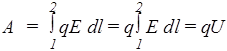Тогда мощность Р равна P=dA/dt= (dq/dt) U, следовательно,

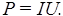(44)

Если вся работа А идет только на нагревание, и на участке нет эдс, напряжение на его концах равно разности потенциалов. Тогда за время dt в проводнике выделится тепловая энергия dQ=P(t)dt = IUdt. Подставляя U=IR, получим: dQ=I²Rdt. Интегрируя, вычисляем полное количество тепловой энергии, выделившееся в проводнике за время t. Это и есть закон Джоуля-Ленца в интегральной форме

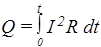. (45)

Если ток постоянен, то выражение упрощается: Q=I²R D t.

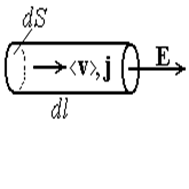
Рис.16

Закон Джоуля-Ленца в дифференциальной форме. Вычислим энергию, которая выделяется в дифференциально малом объеме проводника dV, предполагая для простоты, что векторы j, E и d l направлены одинаково (рис.16). При перемещении заряда dq на расстояние dl поле совершает работу dA=dqEdl. Подставим в это выражение Е из закона Ома: Е=rj, и заряд dq, выраженный через плотность тока: dq=jdtdS. Считая, что вся эта работа идет на нагревание проводника, т.е. dA=dQ, получим

,

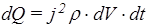где мы учли, что dV=dSdl. Разделив обе части на dVdt, получим величину энергии, выделяющейся в единицу времени в единице объема проводника, которая называется удельной тепловой мощностью тока

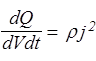. (46)

Формула (46) выражает закон Джоуля-Ленца в дифференциальной форме: удельная тепловая мощность тока пропорциональна квадрату плотности тока в той же точке.
Лекция 5. Магнитное поле в вакууме. Индукция магнитного поля.

В 1820 г Эрстед обнаружил, что магнитная стрелка устанавливается определенным образом по отношению к проводу, по которому идет ток. Эксперименты показали, что вокруг проводника с током существует магнитное поле, вызванное движением зарядов, и наоборот, магнитное поле действует только на движущиеся заряды.

По современным представлениям, магнетизм имеет релятивистскую природу. Изложение этого вопроса выходит за рамки данного курса, однако некоторое представление о релятивистской природе магнетизма можно получить из следующих не строгих соображений.

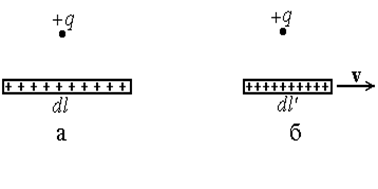
Представим покоящийся заряд q в поле длинной тонкой нити, заряженной с линейной плотностью l> 0 (рис. 17 а). Со стороны электрического поля нити на заряд действует сила отталкивания

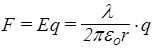(47)

Пусть нить движется вправо со скоростью v (рис.17 б). С точки зрения покоящегося наблюдателя, длина нити уменьшилась. Поскольку заряд - релятивистский инвариант, величина заряда нити не изменилась:

ldl = l¢dl¢, (48)

Рис.17

где dl, dl¢ - элементы длины покоящейся и движущейся нитей соответственно; l¢, - линейная плотность заряда движущейся нити. Учтем в (48) релятивистское сокращение длины ():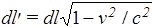

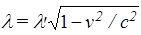, (49)

откуда следует, что l¢ >l. Поэтому должна измениться и сила:

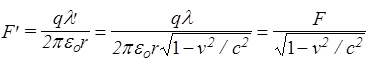, Þ

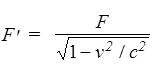. (50)

Умножим обе части последнего равенства на (1- v²/c²), после чего выразим F

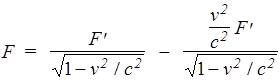. (51)

С точки зрения движущегося вместе с нитью наблюдателя существует только (первое слагаемое) кулоновское отталкивание между зарядом и нитью (второе слагаемое равно нулю). А с точки зрения покоящегося - сила Кулона увеличилась по модулю, но появилась дополнительная, в v²/c² меньше кулоновской, сила притяжения, которая представляет собой так называемую магнитную силу.

Разделив выражение (51) на q, получим аналогичное соотношение для напряженностей

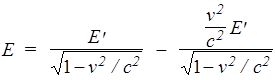. (52)

Дата добавления: 2014-01-04