Лекция 10. Формула Стокса. Уравнения

Магнитное поле движущегося заряда. Чтобы получить удовлетворяющее эксперименту направление и величину магнитной силы вводят вектор индукции магнитного поля В, характеризующий магнитное поле зарядов, движущихся со скоростью v

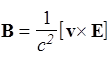. (53)

В нашем примере (с учетом взаимной перпендикулярности векторов скорости и напряженности) B¢=vE ¢ /c², Þ v²E¢/c²=vB¢, что после подстановки во второе слагаемое выражения (52) и умножения обеих частей на 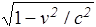дает

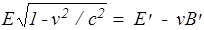. (54)

Это - преобразование Лоренца, показывающее, как изменяются поля при переходе к движущейся системе отсчета и что электрическое и магнитное поля связаны между собой.

С учетом определения (53) и трактовки второго слагаемого в выражении (51), магнитная сила, действующая на заряд q равна

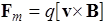. (55)

Эта сила действует только на движущийся заряд, перпендикулярна его скорости, и поэтому работы не совершает. Значит, в постоянном магнитном поле энергия заряженной частицы остается неизменной.

Сила Лоренца. Если заряд одновременно находится в электрическом и магнитном полях, то на него действует результирующая сила

F _л = q E + q [ v´B ], (56)

называемая силой Лоренца. Таким образом, сила Лоренца равна сумме сил, действующих на заряд со стороны электрического и магнитного полей.

Магнитная индукция поля движущегося заряда. Подставим в определение (53) выражение для напряженности электрического поля точечного заряда

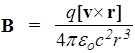. (57)

Введем m_о - магнитную постоянную (m_о =1/ e_оc² =4 p ×10^-7(Гн/м)), и подставим ее в (57). Тогда индукция В магнитного поля движущегося заряда равна

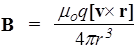. (58)

Пусть два одинаковых заряда движутся параллельно с равными скоростями. Между ними существуют силы электрического и магнитного взаимодействий. Так как B=vE/c² и F_m=qvB, то F_m= qv²E/c²; но F_эл=qE, поэтому F_m/F_эл=v²/c², т.е. магнитная сила слабее электрической в v²/c² раз! Магнетизм исчез бы, если бы скорость света с®¥ и он отсутствует при v®0, т.е. когда заряды покоятся. Следовательно, магнетизм является релятивистским эффектом.

На первый взгляд, этому противоречит следующий экспериментальный факт. Два провода, по которым течет ток в одном направлении, притягиваются, хотя сила электростатического отталкивания движущихся зарядов в v²/c² раз больше силы их магнитного притяжения. Дело в том, что в любом объеме проводника, заряды, создающие ток, в высокой степени скомпенсированы положительными зарядами атомных ядер. Поэтому провод с током практически нейтрален, и наблюдаемое взаимодействие является магнитным.

Принцип суперпозиции магнитных полей. Суммарная магнитная индукция в некоторой точке пространства есть векторная сумма магнитных индукций отдельных полей.

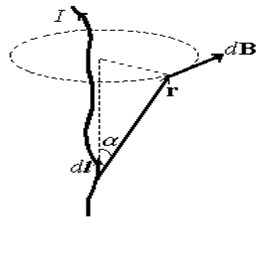
Рис.18

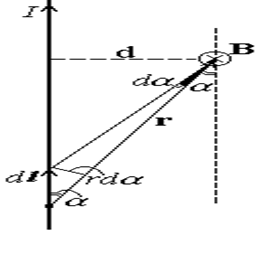
Закон Био-Савара-Лапласа. Так называется соотношение, позволяющее вычислить магнитную индукцию d В в точке с радиус-вектором r, создаваемую элементом d l тонкого провода, по которому течет ток I (рис.18). Пусть S - сечение провода. В выражение (58) для магнитной индукции, создаваемой отдельным зарядом, входит его скорость, очевидно, равная векторной сумме скоростей хаотического и направленного движений. Поскольку обычный ток создается большим числом зарядов, скорости хаотичного движения которых случайны, то случайным будет и соответствующий вклад в магнитную индукцию. Поэтому в среднем магнитное поле, создаваемое вследствие хаотичного движения зарядов, равно нулю. Таким образом, в соответствии с выражением (58), магнитная индукция d B от зарядов, находящихся в элементе dV провода, после усреднения по всем возможным скоростям равна

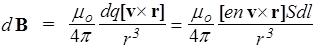. (59)

В последнем равенстве учтено, что dq=en×dl×S, где n - концентрация носителей заряда; v - средняя скорость направленного движения зарядов, создающих ток I. Первый сомножитель в векторном произведении является вектором плотности тока (см. 34): en v = j. Учитывая, что для тонкого провода направления векторов j и d l совпадают, представим вектор j в виде: j = j ×(d l /dl)=(j/dl) d l, где j и dl - модули векторов. Подставим в (59) en v =(j/dl) d l и сократим на dl

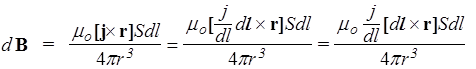, Þ

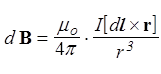. (60)

Это - закон Био-Савара-Лапласа, который позволяет вычислить магнитную индукцию d B, создаваемую элементом d l тонкого проводника с током I в точке с радиусом-вектором r, проведенным из d l. Модуль dB определяется модулем векторного произведения

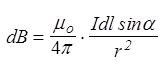, (61)

где a - угол между векторами d l и r.

Закон Ампера. Пусть проводник с током помещен в магнитное поле с индукцией В. Тогда на каждый из носителей тока действует сила Лоренца

F = e [(u + v)´ B ],

где u - скорость хаотического движения, v - направленного. Выделим элемент объема проводника dV=Sdl, где S - сечение, dl элемент длины. Если усреднить силу F по всем носителям в объеме dV, то средняя сила

< F >= e [< v >´ B ],

так как средняя скорость хаотичного движения равна нулю. Если концентрация заряженных частиц n, то число носителей в объеме dV равно ndV=n×dlS, поэтому на элемент dl действует сила

d F = < F > n×dlS = [ en < v >´ B ] dlS.

Учитывая, что j = en < v >, получим d F = [ j ´ B ] Sdl. Поскольку для тонкого провода векторы d l и j параллельны, а jS=I, получаем выражение для силы Ампера

d F = I [ d l ´ B ]. (62)

Соотношение (62), называемое также законом Ампера, позволяет вычислить силу, действующую на элемент тонкого провода d l, по которому течет ток I в магнитном поле с индукцией В.

Поле прямого проводника с током. Рассмотрим бесконечный длинный тонкий прямой провод, по которому течет ток I (рис. 19). Элемент проводника d l создает в точке r магнитное поле в соответствии с законом Био-Савара-Лапласа (60). Очевидно, sina=r×da/dl= d/ r, где d - расстояние от провода до точки. Выражая отсюда dl и r через a и d, получим

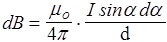. (63)

Рис.19

Мы взяли модуль dB, потому что все d B направлены одинаково (перпендикулярно плоскости рис.19) Интегрируя по a в пределах от 0 до p, получаем магнитную индукцию прямого проводника с током на расстоянии d от него:

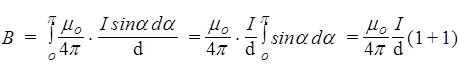, Þ

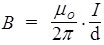. (64)

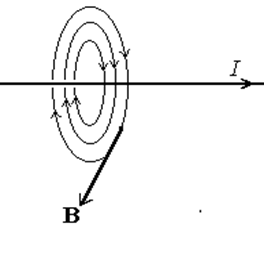
Итак, магнитная индукция от бесконечного прямого провода с током, прямо пропорциональна силе тока и обратно пропорциональна расстоянию от провода. Магнитное поле этого провода изображено на рис.20.

Рис.20

Теперь можно дать определение основной электрической единицы в системе СИ, ампера. Возьмем два параллельных бесконечно длинных проводника с одинаковыми токами I. По закону Ампера на единицу длины каждого проводника будет действовать сила F = IB₁=IB₂, где B₁ и B₂ определяются формулой (64)

.

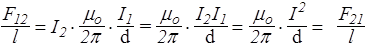Отсюда - определение: ампер [ А ] - это сила неизменяющегося тока, который, проходя по двум параллельным проводникам бесконечной длины и ничтожно малого кругового сечения, расположенных на расстоянии 1 м друг от друга в вакууме, вызывает между ними силу взаимодействия, равную 2×10^-7 Н на каждый метр длины. Кулон [ Кл ]- есть заряд, проходящий за 1 с через поперечное сечение однородного изотропного проводника, по которому течет ток 1 А.

Дата добавления: 2014-01-04