Максвелла в дифференциальной форме

Формула Стокса. Интегрируя выражение (100) по поверхности S, получим циркуляцию: Г= 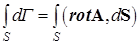. С другой стороны, согласно определению циркуляции, это криволинейный интеграл вдоль границы поверхности S, т.е. вдоль контура L, следовательно

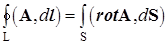. (101)

Это - формула Стокса: циркуляция векторного поля по любому замкнутому контуру равна потоку ротора этого поля через поверхность, ограниченную этим контуром.

Оператор Гамильтона набла. Формулы векторного анализа упрощаются, если ввести, следуя английскому математику Гамильтону, оператор Ñ (набла), символически изображающийся так:

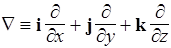. (102)

Если оператор Ñ действует на скалярную функцию j, то получается градиент

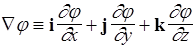. (103)

Если Ñ скалярно умножить на векторную функцию A, - дивергенция:

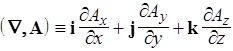. (104)

Векторное произведение Ñ и вектора А дает ротор вектора А

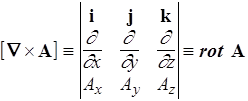. (105)

Запишем с помощью оператора набла формулы Гаусса-Остроградского (94) и Стокса (101)

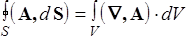, (106)

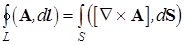. (107)

Уравнения Максвелла в дифференциальной форме. Применим формулу Стокса к первому уравнению Максвелла (см. лекцию 8). Интеграл по замкнутому контуру L в левой части преобразуется в интеграл от ротора E по поверхности, ограниченной этим контуром

.

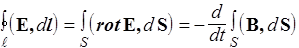Поскольку это равенство справедливо для любой поверхности S, подынтегральные функции должны быть равны

. (108)

Это - дифференциальная форма первого уравнения Максвелла, показывающая, что вихревое электрическое поле порождается изменением во времени магнитного поля в той же точке.

Применим формулу Гаусса-Остроградского ко второму уравнению Максвелла в интегральной форме

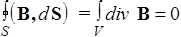
Следовательно,

div B = 0. (109)

Дифференциальная форма второго уравнения Максвелла (109) показывает, что магнитное поле не имеет источников.

Преобразуем левую часть третьего уравнения Максвелла в интегральной форме по формуле Стокса

.

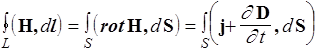Последние два интеграла равны для любой поверхности S только тогда, когда равны подынтегральные функции, следовательно,

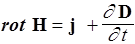. (110)

Дифференциальная форма третьего уравнения Максвелла (110) показывает, что вихревое магнитное поле в каждой точке поля порождается или изменением электрического поля (током смещения), или токами проводимости.

Применим формулу Гаусса-Остроградского к четвертому уравнению Максвелла в интегральной форме

.

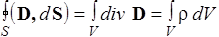Последнее равенство выполняется для любого V, если

div D = r. (111)

Четвертое уравнение Максвелла в дифференциальной форме (111) показывает, что источниками (или стоками) электрического поля являются заряды.

Оператор Лапласа. Уравнение Пуассона. Учитывая, что D= e_o E и E = - grad j, из уравнения (111) получим

.

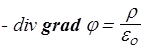Распишем операцию слева подробно

.

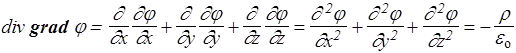Последнюю сумму можно выразить компактно, если ввести дифференциальный оператор Лапласа D (дельта)

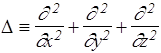. (112)

Тогда уравнение (111) можно записать так:

. (113)

Это - уравнение Пуассона. Оно выражает связь между плотностью заряда в данной точке поля и "ускорением" изменения потенциала в ее окрестности. При r =0 уравнение Пуассона (113) переходит в уравнение Лапласа

D j = 0. (114)

Уравнение непрерывности в дифференциальной форме. Ранее мы получили уравнение непрерывности (83) в интегральной форме. Применим к его левой части формулу Гаусса-Остроградского, а заряд в правой выразим через объемную плотность заряда

.

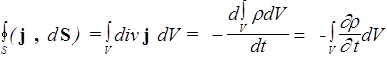Так как объем V произволен, следовательно,

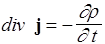. (115)

Это - уравнение непрерывности в дифференциальной форме. Если принять во внимание, что j = r v, где v - скорость направленного движения зарядов, этому уравнению можно придать следующую форму:

, (116)

в которой уравнение непрерывности выражает закон сохранения заряда. В заключение запишем уравнения Максвелла в дифференциальной форме, пользуясь оператором набла

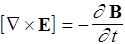I. . II. .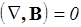

III. . IV. (Ñ, D) = r.

Лекция II. Электрическое поле в веществе.

Уравнений Максвелла недостаточно, чтобы найти поля по данным распределениям зарядов и токов. Их необходимо дополнить так называемыми материальными уравнениями, которые характеризуют свойства среды. Для этого рассмотрим сначала электрическое поле в веществе.

Поместим в электрическое поле плоского конденсатора металлическую пластинку (рис.35). Очевидно, свободные электроны соберутся на поверхности металла вблизи положительно заряженной пластины конденсатора. Поверхность проводника вблизи отрицательно заряженной пластины окажется положительной. Электроны будут двигаться до тех пор, пока результирующее поле Е не станет равным нулю

Е + Е ¢ = 0,

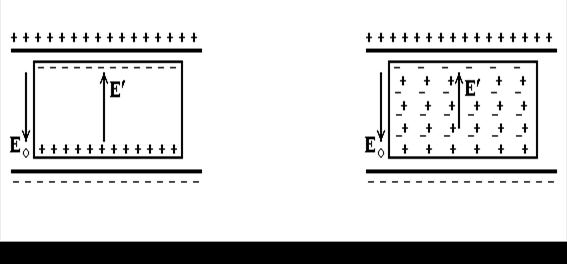
Рис.35 Рис.36

где Е ¢ – поле зарядов пластинки, Е _o - внешнее поле. Если образец -диэлектрик, то картина будет другой (рис.36).

Обычно диэлектриками называют вещества, почти не проводящие электрический ток. Проводимость диэлектриков в I0¹⁵ - I0²⁰ раз меньше, чем у металлов, так как молекулы диэлектрика удерживают свои электроны и собственных свободных зарядов в диэлектрике нет. Заряды, входящие в состав молекул диэлектрика, называются связанными. У симметричных молекул (типа Н₂, О₂,...) центры масс положительных и отрицательных зарядов совпадают, поэтому у них отсутствует собственный дипольный момент. Это - неполярные диэлектрики. Несимметричные молекулы обладают собственным дипольным моментом, и тогда они называются полярными. Полярные и неполярные молекулы в электрическом поле ведут себя по-разному. Молекулы полярного диэлектрика будут поворачиваться подобно диполям. Молекулы неполярного диэлектрика становятся полярными, а затем поворачиваются в поле. Таким образом, молекулы любого диэлектрика будут поворачиваться, ориентируясь собственным или приобретенным дипольным моментом вдоль поля (рис.36). Этот процесс называется поляризацией, и он приводит к возникновению поля связанных зарядов Е ', направленного противоположно внешнему полю Е _о. Результирующее поле в диэлектрике равно

Е = Е _о + Е '. (117)

Напряженность поля плоского конденсатора Е_о = s/e_o. Возникший вследствие поляризации связанный не скомпенсированный заряд появляется только на поверхностях образца, образуя подобие второго конденсатора. Поэтому для однородного образца Е' = s'/e_o (s и s' - поверхностные плотности свободных зарядов пластин и связанных зарядов диэлектрика). Подставляя Е_o и Е ' в (117), получим

, Þ s¢= s - e_oE. (118)

Так как Е_o и Е' направлены противоположно, результирующее поле Е будет меньше Е_o в некоторое e раз: Е = Е_o/e = s/ee_o => s = ee_oЕ. Подставляя s в (118), получим поверхностную плотность связанных зарядов

s¢ = (e - 1) e_oE º x e_oE. (119)

Величина e называется диэлектрической проницаемостью, а x = e -1 - диэлектрической восприимчивостью. Таким образом, на поверхности диэлектрика в электрическом поле появляется связанный заряд, поверхностная плотность которого пропорциональна величине поля в диэлектрике.

Вектор поляризованности. В общем случае степень поляризации диэлектрика характеризуют вектором поляризованности Р, представляющим собой суммарный дипольный момент единицы объема

, (120)

где р _i=q_i l _i. - дипольный момент i -й молекулы, суммирование идет по всем молекулам в объеме D V. Выясним, как связаны Р и s'. Выделим для простоты объем D V в виде прямого параллелепипеда высотой l и площадью основания D S. Пусть диэлектрик поляризован однородно, т.е. все q_i и

l _i - одинаковы в пределах D V (рис.37). Видно, что избыточный связанный заряд остается только на верхней и нижней поверхностях D V, внутри все заряды скомпенсированы. Спроектируем все p _i на направление вектора l:

,

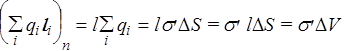Рис.37 Рис.38

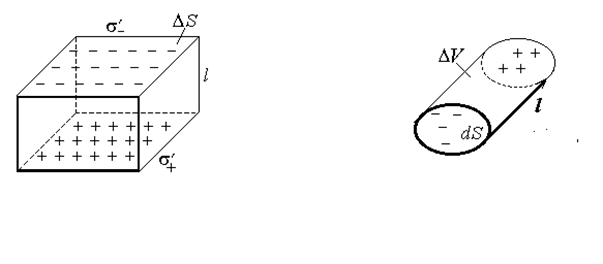
что после деления на D V и перехода к пределу (120) дает P_n. Следовательно, величина нормальной составляющей вектора поляризованности равна поверхностной плотности связанного заряда

P_n = s'. (121)

Поскольку s'=x e₀Е, ® Р_n=x e₀Е_n. Как показывает опыт и расчет, для однородного диэлектрика это верно и в векторном виде

Р =xe_о Е. (122)

Теорема Гаусса для вектора Р. Рассмотрим произвольную замкнутую поверхность S внутри диэлектрика. Построим на ее элементе dS объем D V в виде косого цилиндра (рис.38). Пусть в результате поляризации в объеме D V суммарный положительный заряд сместился относительно суммарного отрицательного на вектор l. Свяжем систему отсчета с центром масс отрицательных зарядов. Тогда поляризованность можно выразить так:

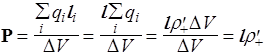, (123)

где r¢₊ - объемная плотность положительного связанного заряда. Вычислим заряд dq', прошедший через dS при поляризации:

dq' = r¢₊ (l, d S),

где объем косого цилиндра выражен в виде скалярного произведения: D V = (l, d S). Внутри исходно нейтрального объема оказался равный прошедшему отрицательный заряд, следовательно, (P, d S) = -dq'. Проинтегрируем это равенство по замкнутой поверхности S:

. (124)

Это - теорема Гаусса для вектора поляризованности Р. Поток вектора Р через любую замкнутую поверхность равен со знаком минус суммарному связанному заряду внутри этой поверхности. Если диэлектрик поляризован однородно и внутри нет свободных зарядов, то сколько зарядов вошло внутрь S столько же и выйдет. Что такое тогда избыточный связанный заряд? Действительно, тогда q' =0. Покажем это. Подставим в (124) выражение для Р (122) и вынесем константы из-под интеграла:

.

Интеграл в левой части равен по теореме Гаусса для вектора Е суммарному заряду (любой природы) внутри замкнутой поверхности S, деленному на e_o; в данном случае - сумме связанных и свободных зарядов. Если свободных зарядов q нет, то

,

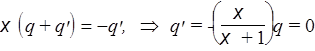следовательно, нет и связанных зарядов.

Применив теорему Гаусса-Остроградского к левой части (124), получим для любого объема V

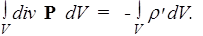
откуда следует, что равны и подынтегральные выражения

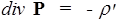. (125)

Таким образом, источниками вектора Р являются нескомпенсированные объемные связанные заряды, возникшие вследствие поляризации.

Формулируя теорему Гаусса для вектора Е, мы не конкретизировали природу зарядов. Значит, следует учитывать и связанные, и свободные заряды, а именно

,

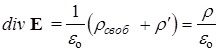где r - объемная плотность всех зарядов, r_своб - только свободных. Подставляя в последнюю формулу выражение для r' (125), получаем

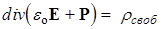. (126)

Вектор в скобках называется электрическим смещением или электрической индукцией D

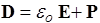. (127)

Ранее для вакуума мы ввели D = e_o E, которое согласуется с последним определением, так как в вакууме Р =0. Из (126) следует, что

,

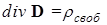т.е. источниками вектора D являются свободные заряды. Подставляя в (127) Р из (122), получим D = e_о E + e_оx E = e_o E (1+ x). Величина e =I+ x называется диэлектрической проницаемостью вещества. Таким образом, в веществе

D = ee_o E. (128)

Поскольку в вакууме D = e_o E, то диэлектрическая проницаемость e показывает, во сколько раз ослабляется электрическое поле в веществе по сравнению с вакуумом. Следует подчеркнуть, что последнее верно только для изотропного диэлектрика. В общем случае e - тензор и векторы Е и D - не коллинеарны.

Лекция 12. Условия на границе раздела диэлектриков. Энергия электрического поля

Введение вспомогательного вектора D позволило вынести описание поляризации диэлектрика за рамки уравнений Максвелла. Поле вектора D можно изображать с помощью силовых линий, направление и густота которых определяются также, как и для вектора Е. Однако линии вектора Е могут начинаться как на свободных, так и на связанных зарядах. Поскольку источниками вектора D являются только свободные заряды, на них начинаются и заканчиваются линии вектора D. Через области поля, содержащие связанные заряды, линии вектора D проходят, не прерываясь.

В качестве иллюстрации полезности вектора D рассмотрим пример. Пусть точечный свободный заряд q находится в центре шара радиуса R из однородного изотропного диэлектрика с диэлектрической проницаемостью e. Найдем напряженность Е поля как функцию расстояния r от центра.

В этой задаче невозможно воспользоваться теоремой Гаусса для вектора Е, несмотря на то, что симметрия задачи располагает к этому, потому что не дано распределение связанного заряда. Однако поток вектора D зависит только от свободного заряда, который дан. Поэтому сначала применим теорему Гаусса для вектора D, выбрав в качестве гауссовой поверхности сферу произвольного радиуса r

4pr²D = q.

Подставляя D=ee_oE для r£R и D=e_oE для r >R, получаем

при r £ R;

Рис.39

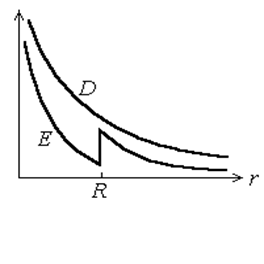
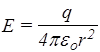при r > R.

Из сопоставления последних двух формул (они отличаются множителем e в знаменателе) видно, что при r = R величина Е испытывает скачок. Графики зависимостей Е и D от r представлены на рис.39.

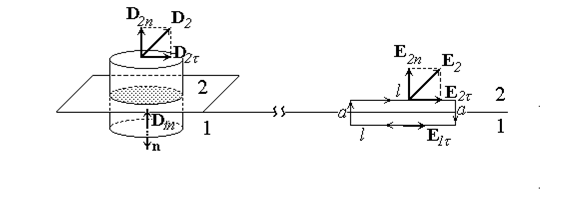
Условия для векторов E и D на границе раздела диэлектриков. Выясним, как связаны компоненты векторов E и D по разные стороны от границы диэлектриков 1 и 2 (рис.40). Пусть S - цилиндрическая поверхность пренебрежимо малой высоты. Поток вектора D через S равен нулю, так как внутри нее нет свободных зарядов. Поток через боковую поверхность очень мал, так как мала ее площадь. Поэтому поток через нижнее основание равен потоку через верхнее основание: 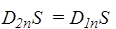, Þ

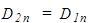. (129)

Рис.40 Рис.41

Таким образом, нормальная составляющая D_nсохраняется.

Рассмотрим теперь прямоугольный замкнутый контур (рис.41), сторона которого l параллельна границе раздела, а высота а много меньше длины. Так как циркуляция вектора Е электростатического поля равна нулю, для изображенного на рисунке контура это значит, что , следовательно,

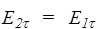, (130)

т.е. при переходе через границу раздела диэлектриков сохраняется тангенциальная составляющая E_t.

Покажем, что величины составляющих E_n и D_t меняются на границе раздела. Поскольку векторы Е и D связаны соотношением (128), и D_n сохраняется, следовательно, e₂E_2n = e₁E_1n, или

. (131)

Аналогично из (128) и сохранения Е_t следует, что

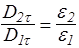. (132)

Из граничных условий в частности следует, что если диэлектрик заполняет все пространство, занимаемое полем (например, в плоском конденсаторе), то напряженность поля Е в нем будет в e раз меньше, чем в отсутствие диэлектрика.

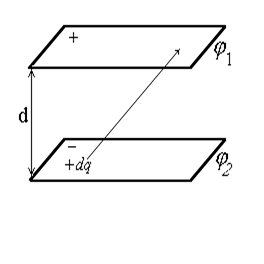
Рис.42

Энергия электрического поля. Рассмотрим процесс зарядки конденсатора (рис.42). Пусть верхняя пластина заряжена положительно зарядом + q до потенциала j₁, а нижняя-- зарядом -q до j₂. Работа против сил поля при переносе заряда dq >0 с нижней пластины на верхнюю идет на увеличение энергии взаимодействия зарядов

dW = - dA = dq (j₁ -j₂) = dq U.

Выразим напряжение U через емкость С: U=q/С, тогда dW=qdq/C. Интегрируя, получаем энергию электрического поля заряженного конденсатора

. (133)

Как известно, емкость плоского конденсатора С=ee_oS/ d, где S - площадь одной пластины, d - расстояние между пластинами. Подставим С в (133) и учтем, что напряженность однородного поля между пластинами равна Е=U/ d

,

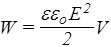где V=S d - объем пространства между пластинами. Отношение W/V характеризует энергию единицы объема и называется плотностью энергии электрического поля

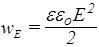(134)

Если поле неоднородно, то плотность энергии электрического поля равна производной w_E=dW/dV. Учитывая, что Е = D /ee_о, a D = e _о Е + Р запишем

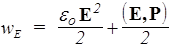. (135)

Полученное выражение представляет собой сумму плотности электрической энергии в вакууме и плотности энергии поляризации диэлектрика. Следовательно, электрическая энергия локализована в самом поле: как там, где есть вещество, так и там, где его нет. Однако если поле стационарно, то при исчезновении порождающих его зарядов, исчезает и само поле. Независимо от породивших их зарядов могут существовать только переменные поля.

Дата добавления: 2014-01-04