Лекция 13. Магнитное поле в веществе. Намагниченность

Установлено, что молекулы многих веществ обладают собственным магнитным моментом, обусловленным внутренним движением зарядов. При отсутствии внешнего магнитного поля магнитные моменты молекул ориентированы беспорядочно, поэтому их результирующее магнитное поле равно нулю.

Если вещество поместить в магнитное поле В _о, то магнитные моменты его молекул приобретают преимущественную ориентацию и суммарный магнитный момент становится отличным от нуля. В результате возникает собственное магнитное поле магнетика B ¢.

Намагниченность. Для описания намагничивания вводят векторную величину J - намагниченность, определяемую магнитным моментом единицы объема магнетика

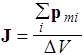, (136)

где p _mi - магнитный момент отдельной молекулы магнетика, суммирование производится по всем молекулам в физически бесконечно малом объеме D V. Внешнее поле ориентирует каждый магнитный момент вдоль поля (аналогично поведению контура с током в магнитном поле). Результирующее поле В в магнетике является векторной суммой внешнего поля В _о и поля В ', создаваемого молекулярными токами

В = В _о + В ', (137)

где В _o = m_o Н. Если во всех точках вектор J одинаков, то говорят, что вещество намагничено однородно.

Рис.43

Для описания поля молекулярных токов рассмотрим цилиндрический образец магнетика длины l и площадью сечения S, такой что l ²>> S. Под действием однородного внешнего поля В _o (рис.43) плоскости молекулярных токов будут стремиться расположиться перпендикулярно вектору В _o. На внутренних участках сечения соседние молекулярные токи направлены навстречу друг другу и поэтому компенсируются. Нескомпенсированными будут лишь молекулярные токи, выходящие на боковую поверхность. Их сумма составляет поверхностный молекулярный ток I ¢, создающий внутри цилиндра магнитное поле В', подобное полю соленоида В'=m_oI'/l (для соленоида В=m_onI, где nI - ток, приходящийся на единицу длины, что для цилиндра равно I'/l. Магнитный момент тока намагничивания I' равен: р_m= I'S=I'lS/l=I'V/l, где V - объем магнетика. Отсюда магнитный момент единицы объема равен

.

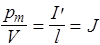Таким образом, В'=m_oj, что для многих магнетиков верно и в векторном виде

В '=m_o J.

Подставляя в (137) В _o и В ', получим результирующее поле в магнетике

B = m_o H + m_o J. (138)

У большинства слабых магнетиков намагниченность пропорциональна напряженности магнитного поля

J = c H. (139)

Безразмерная величина c называется магнитной восприимчивостью. Подставляя (139) в (138), получим

.

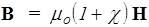Величина m=I+c, - также безразмерная, называется магнитной проницаемостью вещества. Таким образом, в магнетике

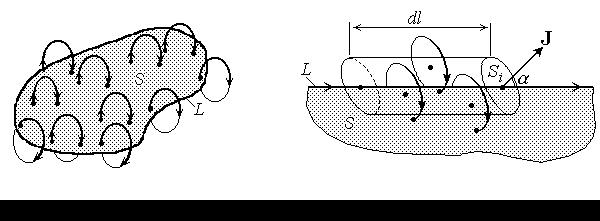
B = mm_o H. (140)

Рис.44 Рис.45

Вычислим сумму токов намагничивания 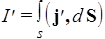, где j ¢ - плотность этого тока. Выберем в магнетике произвольный контур L, ограничивающий поверхность S. Как видно из рис.44, микротоки могут быть двух типов: одни пронизывают поверхность S дважды в противоположных направлениях, другие - один раз и как бы нанизаны на границу L. Первые в сумме дают ноль, вторые складываются в ток намагничивания. Очевидно, нанизанными окажутся токи, попавшие внутрь косого цилиндра объемом dV=S_idl×cosa (рис.45), где dS_i - площадь i -го молекулярного тока, a - угол между J и элементом dl контура. Сумма токов dI¢ = I_i¢×ndV, где n - концентрация. Так как dV =S_idlcosa, то dI'=nI_i¢×S_i×dlcosa, где первые три сомножителя представляют собой модуль магнитного момента единицы объема, т.е. намагничивание. Так как произведение модулей двух векторов на косинус угла между ними есть скалярное произведение, следовательно, dI'= (J, d l). Интегрируя вдоль L, получаем

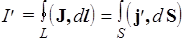. (141)

Циркуляция вектора намагниченности равна сумме микротоков намагчивания. Применяя к (141) формулу Стокса, получим:

rot J = j ¢. (142)

Циркуляция вектора Н в присутствии магнетика. Поскольку в магнетике вектор В определяется токами проводимости I и токами намагничения I¢, теорема о циркуляции вектора В должна выглядеть так

.

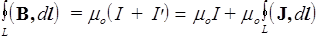Вычислить I¢ весьма сложно. Чтобы его избежать, перепишем последнее выражение следующим образом:

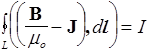. (143)

Вектор, равный

H = B /m_o - J, (144)

называется вектором напряженности магнитного поля в веществе. Поскольку в отсутствие вещества J º0, это определение согласуется с ранее введенным для вакуума Н = В /m_o; и теорема о циркуляции вектора Н может быть записана так

.

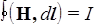Учитывая, что вектор Н может появляться еще и за счет токов смещения, окончательной формулировкой будет следующая:

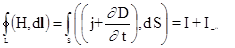. (145)

Циркуляция вектора Н по произвольному контуру равна сумме всех токов проводимости и смещения, охватываемых этим контуром.

Граничные условия для векторов B и H. Выделим на границе раздела магнетиков 1 и 2 цилиндр дифференциально малой высоты (рис.46). Тогда потоком вектора В через боковую поверхность можно пренебречь, и полный поток наружу из этого цилиндра равен

B_2n D S + B_1n’ D S = 0,

или с учетом того, что n =- n¢, после сокращения на D S имеем

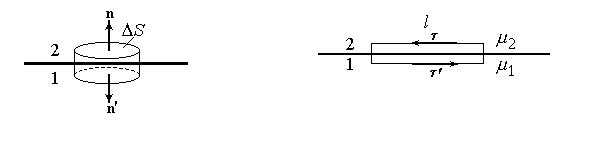
B_2n = B_1n, (146)

т.е. нормальная составляющая вектора В сохраняется.

Рис.46 Рис.47

Применим теорему о циркуляции вектора H к прямоугольному контуру длины l и пренебрежимо малой высоты (рис.47) H_2tl+ H_1t¢ l= 0. Учитывая, что t =- t¢, получаем граничное условие для вектора H

H_2t = H_1t. (147)

Очевидно, на границе раздела однородных магнетиков вектор B ведет себя аналогично вектору D, а вектор H - аналогично вектору E. Поэтому с учетом соотношения (140) для остальных составляющих получаем

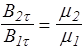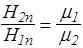, . (148)

Таким образом, тангенциальная составляющая вектора B и нормальная составляющая вектора Н испытывают скачок при переходе границы раздела двух магнетиков.

Классификация магнетиков. Все магнетики делятся на слабомагнитные (пара- и диамагнетики) и сильномагнитные (ферромагнетики).

Диамагнетики. В грубом приближении электрон в атоме движется по орбите подобно волчку. Как известно из механики, в этом случае возникает прецессия орбиты, т.е. вращение вектора р _m вокруг В. Расчет показывает, что для однородного внешнего поля угловая скорость прецессии одинакова для всех электронов. Вследствие этого возникает дополнительный индуцированный магнитный момент, направленный против поля, р _m ¢~- В. Это и есть причина диамагнетизма. Если атомы обладают собственным магнитным моментом, то поле оказывает на них ориентирующее действие. Возникающий вследствие ориентации результирующий магнитный момент р_m >> р_m ¢. Поэтому диамагнитными свойствами обладают только те вещества, молекулы которых не имеют собственного магнитного момента. Магнитная проницаемость диамагнетиков - m£1, а магнитная восприимчивость - c=m- I, очевидно, немного меньше нуля.

Парамагнетики. Парамагнетиками называются вещества у которых магнитный момент молекул р _m ¹ 0. Если парамагнетик внести в магнитное поле, то последнее будет стремиться упорядочить магнитные моменты молекул параллельно вектору В поля, а тепловое движение, напротив, разбросать. В результате возникает некоторая преимущественная ориентация. Экспериментально установленный закон Кюри показывает, что магнитная восприимчивость парамагнетиков обратно пропорциональна абсолютной температуре

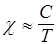. (149)

где С - постоянная Кюри, зависящая от структуры вещества. Для парамагнетиков c >0, а m> I.

Рис.48

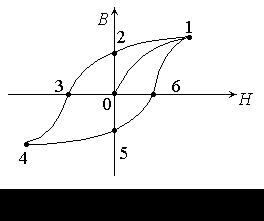
Ферромагнетики. Для ферромагнетиков зависимость В (Н) нелинейна и неоднозначна, поэтому формально вводят m=В/m_oН=f(H), но при этом m имеет смысл только в ходе первоначального намагничивания (см. участок 0®1 на рис.46). Максимальное значение m у ферромагнетиков может быть очень велико, например, у железа m»5000. На рис.48 представлена кривая намагничивания для типичного ферромагнетика. При первоначальном увеличении H индукция магнитного поля возрастает до некоторой величины (участок 0®I). Затем при уменьшении напряженности до нуля индукция магнитного поля не спадает до нуля (I®2). Это остаточное намагничивание объясняет существование постоянного магнита. Увеличение Н в противоположном направлении (2®3) приводит к полному размагничиванию, а затем и к перемагничиванию, т.е. переориентации магнитных моментов в противоположном направлении (3®4). Затем при уменьшении Н кривая идет по пути 4®5. При Н=0 (в точке 5) В¹0. Уменьшение В до нуля происходит при возрастании Н в первоначальном направлении (5®6). Намагничивание по пути 6®I отличается от первоначального 0®1 и указывает на неоднозначность зависимости В (Н). Ферромагнетизм нельзя объяснить в рамках классической электродинамики. Оказалось, что в ферромагнетике действуют межатомные силы, имеющие квантовую природу, которые ориентируют спиновые магнитные моменты электронов в атомах параллельно друг другу. Области с параллельно направленными магнитными моментами называются доменами. Типичный размер домена» 10^-4 см. Во внешнем магнитном поле магнитные моменты доменов ориентируются по полю, значительно увеличивая магнитную индукцию в ферромагнетике. При достаточной величине внешнего поля практически все домены ориентируются вдоль него. При снятии внешнего поля не все домены разориентируются, поэтому для ферромагнитных материалов характерно сохранение остаточной намагниченности.

Дата добавления: 2014-01-04