
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция 15. Электромагнитные волны. Вектор Умова-Пойнтинга
|
|
|
|
Итак, изменяющееся магнитное поле порождает электрическое, а переменное электрическое - магнитное. Таким образом, эти переменные поля не могут существовать по отдельности: любое переменное поле (Е или В) всегда является электромагнитным. Более того, из уравнений Максвелла следует, что электромагнитное поле, возбужденное в ограниченной области, будет распространяться в пространстве, т.е. существовать в форме электромагнитных волн. Выясним, как это получается.
Запишем уравнения Максвелла для однородной непроводящей среды с магнитной проницаемостью m и диэлектрической e. Это значит, что в уравнения Максвелла следует подставить r =0, j =0, В =mm0 Н, D =ee0 Е, что удобно представить в таблице 3
Уравнения Максвелла в дифференциальной форме. Таблица 3
| Уравнения Максвелла, общий случай | № | Уравнения Максвелла при r = 0, j= 0 |

| I | 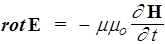
|
| div B= 0 | II | div H= 0 |
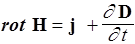
| III | 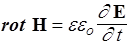
|
| div D = r | IV | div E =0 |
Далее будем иметь дело с уравнениями правой колонки. Вычислим rot от первого уравнения, используя символ Ñ
[ Ñ ´[ Ñ ´ E ]] = Ñ (Ñ,E) - E (Ñ,Ñ). (152)
Эта формула отражает свойство двойного векторного произведения, известное под мнемонически удобным названием “ bac - cab ”:
[ a ´[ b ´ c ]] = b (a,c) - c (a,b).
Ñ(Ñ,E)=0, так как (Ñ,E)= div Е =0, в соответствии с IV-тым уравнением. E (Ñ,Ñ)=(Ñ,Ñ) E = div grad Е =D Е. Таким образом,
[ Ñ ´[ Ñ ´ E ]] = - D Е. (153)
Это rot от левой части первого уравнения Максвелла. Операция rot от правой части после изменения порядка дифференцирования дает
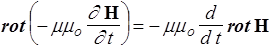 . (154)
. (154)
Подставляя rot H из III уравнения Максвелла и собирая вместе правую и левую части, имеем D Е =mm0 ee0 ¶2 Е /¶t2, или в подробной записи
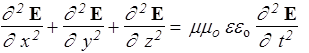 . (155)
. (155)
Это - волновое уравнение. Повторив описанные действия, легко получить такое же уравнение для вектора H
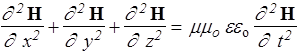 . (156)
. (156)
Каждое из волновых уравнений (155),(156) описывает волну, распространяющуюся с фазовой скоростью v, величина которой определяется коэффициентом при второй производной по времени 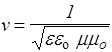 . Так как для вакуума e= 1, m= I, то скорость электромагнитной волны в вакууме
. Так как для вакуума e= 1, m= I, то скорость электромагнитной волны в вакууме 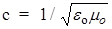 = 3×108 м/с. С учетом этого
= 3×108 м/с. С учетом этого
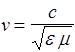 , (157)
, (157)
откуда видно, что фазовая скорость распространения электромагнитной волны в среде в 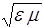 раз меньше, чем в вакууме. Важно, что эта скорость одинакова для Е и Н: электромагнитное поле и возникает, и распространяется как неразрывное целое своих электрической и магнитной частей.
раз меньше, чем в вакууме. Важно, что эта скорость одинакова для Е и Н: электромагнитное поле и возникает, и распространяется как неразрывное целое своих электрической и магнитной частей.
Плоская электромагнитная волна. Рассмотрим электромагнит-ную волну, идущую вдоль оси х. Это значит, что все компоненты векторов Е и Н зависят только от х, а все производные по у и z равны нулю. Тогда
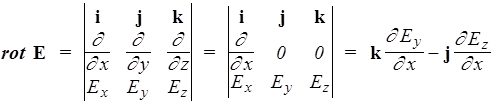 . (158)
. (158)
Аналогично
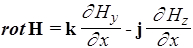 . (159)
. (159)
Учтем эти соотношения в правой колонке табл. 3, принимая во внимание, что уравнения I и III - векторные: каждое из них представляет собой совокупность трех скалярных. Справа от каждого уравнения дадим краткий комментарий.
Уравнения Максвелла для плоской электромагнитной волны. Таблица 4
I. 0=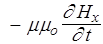 , Þ , Þ
| Hx не зависит от времени |
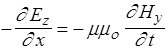 , Þ , Þ
| изменение во времени Нy вызывает распространение Еz вдоль х |
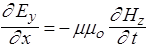 , Þ , Þ
| изменение во времени Нz вызывает распространение Еy вдоль х |
II. 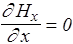 , Þ , Þ
| Hx не зависит от х |
III. 0 = 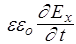 , Þ , Þ
| Еx не зависит от времени |
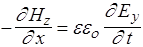 , Þ , Þ
| изменение Еy во времени порождает распространение Нz вдоль х |
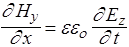 , Þ , Þ
| изменение Еz во времени порождает распространение Нy вдоль х |
IV. 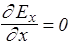 , Þ , Þ
| Ex не зависит от х |
Суммируем комментарии: Нx и Еx не зависят от времени и координаты х, являясь тем самым некоторыми постоянными составляющими электрического и магнитного полей. Прибавление постоянных величин к решениям волновых уравнений (155) и (156) повлияет только на значения констант в общем решении. Поскольку эти константы все равно придется получать из начальных условий, здесь допустимо положить Нx и Еx, равными нулю.
Остальные уравнения показывают, что изменение Нy связано с изменением Еz, а изменение Еy - только с изменением Нz; например, если в некоторый начальный момент возбудить изменение Еy, то появится Нz, а Нy - нет. Выпишем только те два уравнения, которые связывают Еy и Hy
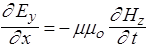 , (160)
, (160)
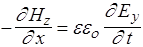 . (161)
. (161)
Продифференцируем первое из этих уравнений по х, изменим порядок дифференцирования по х и по t, а затем подставим ¶Нz / ¶х из второго уравнения
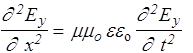 . (162)
. (162)
Аналогично получаем уравнение для Нz
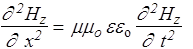 . (163)
. (163)
Это - простейшие дифференциальные уравнения для волны. Как известно, эти уравнения имеют общие решения
Ey = Em cos (wt - kx + a1), (164)
Hz = Hm cos (wt - kx + a2), (165)
где k=w/v - волновое число, a1 и a2 - начальные фазы. Подставим эти решения в уравнения (160) и (161)
kEm sin (wt - kx + a1) = mmow Hm sin (wt - kx + a2),
kHm sin (wt - kx + a2) = eeow Em sin (wt - kx + a1).
Поместим начало координат в точку, соответствующую t =0
kEm sina1 = mmow Hm sina2,
kHm sina2 = eeow Em sina1.
Последнее может совместно выполняться, только если a1=a2, откуда
kEm=mm0wHm,
ee0wЕm=kHm.
Перемножая левые и правые части последних уравнений, получаем
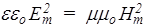 .
.
Таким образом, колебания Е и Н в электромагнитной волне происходят в одной фазе, а амплитуды Еm и Нm связаны соотношением
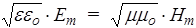 . (166)
. (166)
Решения (164) и (165) можно записать окончательно в векторном виде
E º j Ev = E mcos (wt - kx), (167)
H º k Hz = H mcos (wt - kx). (168)
|
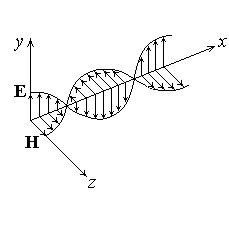
| Рис.50 |
На рис.50 представлена соответствующая этим решениям электромагнитная волна в некоторый момент времени. Векторы Е, Н и v образуют правовинтовую систему и в каждой фиксированной точке пространства изменяются со временем по гармоническому закону. Изменения этих векторов в разных точках пространства происходят со сдвигом фаз, который определяется расстоянием между этими точками. Однако в любой данной точке колебания векторов Е и Н происходят синхфазно: оба вектора одновременно достигают своих максимумов, минимумов и нулевых значений.
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 1193; Нарушение авторских прав?; Мы поможем в написании вашей работы!