Property of limits

Limit and continuity of the function of two variables.

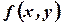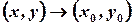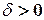Definition 4.1: The limit of function as is a number if for any there exists a such that for all points in domain of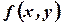, from 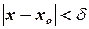and.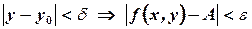

The following rules hold if, .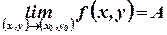

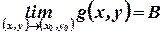Sum rule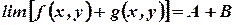
Difference rule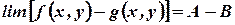
Product rule
Constant multiple rule	,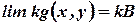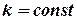
Quotient rule	if

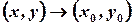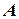All limits are to be taken as and and are to be real.

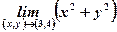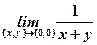Example 4.1. Find limits of the functions: a), b), c)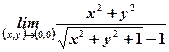

Solution:

a)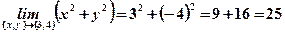

b); c)

=.

Definition 4.2: A function 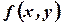is said to be continuous at the point 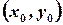if:

1) 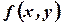is defined at ,

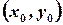2) exist,

3).

For function 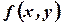fair all properties of the continuous functions similar to functions of one variable. For example, function is continuous everywhere, except a point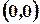. For functionthe points of discontinuity are all points for which or.

Дата добавления: 2014-01-04