
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Определение погрешностей при прямых измерениях
|
|
|
|
Измерение физических величин и классификация погрешностей
В физическом практикуме каждая из лабораторных работ посвящается воспроизведению опытов для наблюдения физических явлений или законов, изучению различных свойств веществ. Свойства тел или физических явлений, которые количественно могут отличаться у разных тел или изменяться у одного и того же тела, называются физическими величинами. К таким величинам относятся масса, объем, длина, температура, давление, скорость, ускорение, плотность и т.д.
Как правило, при выполнении лабораторных работ необходимо производить измерения той или иной физической величины, характеризующей рассматриваемое явление, закон или свойство изучаемого вещества. Измерить какую-либо физическую величину - это значит узнать, сколько раз заключается в ней однородная величина, принятая за единицу измерения. Измерения разделяют на прямые и косвенные.
При прямых измерениях определяемая величина сравнивается с единицей измерения непосредственно или при помощи измерительного прибора проградуированного в соответствующих единицах. Примерами прямых измерений является измерение длины линейкой или штангенциркулем, измерение времени секундомером, величины электрического тока амперметром, напряжения вольтметром, сопротивления омметром, температуры термометром и т.д.
При косвенных измерениях определяемая величина находится из результатов прямых измерений тех величин, которые связаны с определяемой величиной функциональной зависимостью. Например, чувствительность осциллографа определяется выражением:
 ,
,
где l - длина светящейся линии на экране осциллографа, расположенная вдоль оси X или Y; Uэф - эффективное напряжение, подаваемое на соответствующий вход (X или Y) прибора. Параметры l и Uэф можно определить прямыми измерениями, используя линейку и вольтметр, а величину S - из указанной выше функциональной зависимости.
Физическую величину невозможно измерить абсолютно точно, поскольку любое измерение сопровождается той или иной ошибкой (погрешностью).Погрешности измерений бывают систематические и случайные.
Погрешность, сохраняющая величину и знак от опыта к опыту, называется систематической. Систематическая погрешность может оставаться постоянной и закономерно изменяться как при изменении одной и той же величины, так и при изменении в некотором диапазоне, например, в диапазоне измерения прибора. По происхождению систематические погрешности можно классифицировать на следующие:
1. Методические (теоретические) погрешности, связанные с недостаточно точным обоснованием самого метода измерения, с допущениями при выводе формул, с зависимостью измеряемой величины от параметров приборов и т.д.
2. Инструментальные погрешности, связанные с конструктивными недостатками прибора, неисправностью или неправильной градуировкой прибора и т.д.
3. Погрешности установки, возникающие из-за неправильной установки прибора и неточной установки стрелки на ноль.
4. Личные погрешности (субъективные), проявляющиеся из-за индивидуальных особенностей экспериментатора при отсчете измеряемой величины (из-за неправильного расположения экспериментатора относительно прибора, неточность интерполяции показания в пределах одного деления и т.д.).
5. Погрешности, вызываемые изменением внешних условий (изменение температурных, магнитных и электрических полей, частоты, напряжения, давления, влажности, ускорения и т.д.).
Погрешность, которая непредсказуемым образом изменяет свою величину и знак от опыта к опыту, называется случайной. Случайная погрешность является результатом действия большого числа случайных причин на каждое измерение, величина и природа которой остается неопределенной. Случайный характер этих погрешностей проявляется в том, что при многократном повторении опыта в одинаковых условиях и с одинаковой тщательностью получаются различные результаты. Погрешности, возникающие в результате неправильного отсчета по шкале прибора, неверной записи отсчетов, грубых нарушений условий измерения и т.д., называются промахами. Измерения, содержащие промахи, не учитываются. В подобных случаях делается повторное (контрольное) измерение.
В основе теории определения погрешностей лежат два положения, подтвержденные опытом.
1. При большом числе измерений физической величины случайные погрешности одинаковой величины, но разного знака встречаются одинаково часто.
2. Погрешности большие по абсолютной величине встречаются реже, чем малые, т.е. вероятность появления погрешности уменьшается с ростом величины погрешности.
Допустим, что мы произвели n прямых измерений некоторой физической величины А, истинное значение которой нам неизвестно. Обозначим через А1, А2, А3,... Аn результаты отдельных измерений. Абсолютную погрешность DАn n-го измерения, представляющую собой разность между истинным значением А и измеряемой величиной Аn, можно записать следующим образом: DАn=А-Аn, тогда результаты отдельных измерений можно представить в виде:
 ,
,  , …,
, …,  (1)
(1)
Абсолютные погрешности DА1, DА2,... DАn могут принимать как положительные, так и отрицательные значения. Суммируя левую и почленно правую стороны равенства (1), получаем:
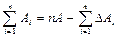 (2)
(2)
Разделив обе стороны равенства (2) на число n и учитывая, что среднеарифметическая величина:
 (3)
(3)
|
 (4)
(4)
Так как в серии большого числа измерений всякой положительной погрешности можно сопоставить равную ей по абсолютной величине отрицательную погрешность, то на основании положения 1, указанного выше,
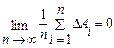 (5)
(5)
|
при 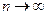
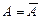 (6)
(6)
|
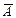 будет отличаться от истинного значения А, т.е. равенство (6) будет приближенным:
будет отличаться от истинного значения А, т.е. равенство (6) будет приближенным:
 (6а)
(6а)
|
 (7)
(7)
|
 (7а)
(7а)
где 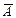 определяется выражением (3), а для определения
определяется выражением (3), а для определения 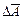 используется формула:
используется формула:
 (8)
(8)
Отношения 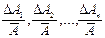 называются относительными ошибками отдельных измерений.
называются относительными ошибками отдельных измерений.
Отношение средней абсолютной ошибки результата к среднему значению дает среднюю относительную ошибку измерений
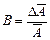 (9)
(9)
Так как относительную ошибку принято выражать в процентах, то
 (9а)
(9а)
|
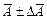 истинных значений измеряемой величины, а интервал, в котором находится единственное значение этой величины.
истинных значений измеряемой величины, а интервал, в котором находится единственное значение этой величины.
Более точную формулу для вычисления абсолютной ошибки результата дает теория вероятностей:
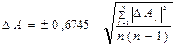 (10)
(10)
Абсолютная ошибка, определяемая уравнением (10), называется наиболее вероятной ошибкой.
Окончательное значение измеряемой физической величины в этом случае записывается следующим образом:
 (11)
(11)
Окончательный результат (11) можно записать с учетом среднеквадратичной ошибки, которая определяется уравнением:
 (12)
(12)
Пример. Определить абсолютную и относительную погрешность диаметра свинцового шарика по пяти измерениям, результаты которых указаны ниже.
| d,мм | 1,47 | 1,46 | 1,43 | 1,45 | 1,44 |
Среднее из пяти найденных значений:
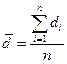
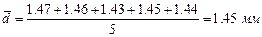
Абсолютные ошибки отдельных измерений:
D d 1 = 1,45 - 1,47 = -0,02 мм
D d 2 = 1,45 - 1,46 = - 0,01 мм
D d 3 = 1,45 - 1,43 = 0,02 мм
D d 4 = 1,45 - 1,45 = 0,00 мм
D d 5 = 1,45 - 1,44 = 0,01 мм
Средняя абсолютная ошибка результатов:
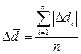
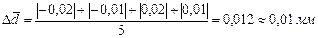
Относительная ошибка:


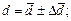
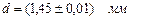 Результат измерений:
Результат измерений:
Аналогично можно произвести обработку результата измерений с наиболее вероятной ошибкой или с учетом средней квадратичной ошибки, используя формулу (10) или (12).
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 6921; Нарушение авторских прав?; Мы поможем в написании вашей работы!