Определение погрешностей при косвенных измерениях

Когда физическая величина не может быть измерена непосредственно, то в этом случае прибегают к косвенным измерениям.

Например, для нахождения величины А пришлось измерить какие-то величины x, y, z. Величина А связана функциональной зависимостью с величинами x, y, z:

А = f (x, y, z)

При косвенных измерениях средняя абсолютная ошибка 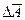может быть найдена по правилам дифференцирования, если знак дифференциала d заменить знаком ошибки D и выбирать знаки таким образом, чтобы величина ошибки была максимальной, т.е.

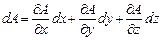(1)

(1)

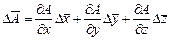(2)

и (2)

Если А является функцией одной переменной x, то

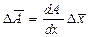
т.е. абсолютная ошибка функции равна абсолютной ошибке аргумента, умноженной на производную этой функции по этому аргументу.

Относительная ошибка, как и при прямых измерениях, определяется формулой:

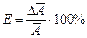
Учитывая, что дифференциал натурального логарифма

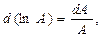
то 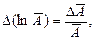(3)

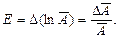или (4)

Приходим к выводу: относительная ошибка результата равна полному дифференциалу натурального логарифма функции, определяющей зависимость данной величины от измеряемых величин.

Для определения относительной ошибки измерения рекомендуется следующая последовательность:

1. Прологарифмировать расчетную формулу.

2. Найти от логарифма полный дифференциал.

3. Сгруппировать все члены, содержащие одинаковый дифференциал (если такие члены есть), и выражения в скобках, стоящие перед дифференциалом, взять по модулю.

4. Знак дифференциала d заменить на знак ошибки D.

5. Выбрать знаки так, чтобы относительная ошибка была максимальной.

Пример. Определить абсолютную и относительную погрешности по единичным измерениям соответствующих аргументов коэффициента h вязкости касторового масла при t=25,5°С, определенного методом Стокса. Величина коэффициента вязкости в этом случае определяется формулой:

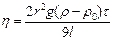, (5)

где r - радиус шарика, g - ускорение свободного падения, r - плотность свинца, r_о - плотность касторового масла, l - расстояние пройденное шариком, t - время движения шарика.

В результате измерений получим:

l = 0,75 м, измеренное с точностью до 0,005 м.

r = 2,0 × 10^-3 м, измеренное с точностью до 0,1×10^{-4 м.}

t = 5,96 с, измеренное с точностью до 0,01 с.

r - r_o = 10320 кг/м³, измеренное с точностью до 0,5 кг/м³.

g = 9,8 м/с², измеренное с точностью до 0,05 м/с².

Обработка результатов измерений:

1. Определим коэффициент h вязкости, используя выражение (5):

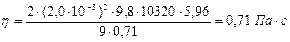
2. Логарифмируя выражение (5), получим:

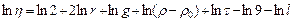
3. Дифференцируем полученное выражение:

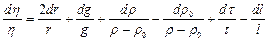
4. Заменяем знак дифференциала d на знак приращения D и находим максимальную относительную погрешность:

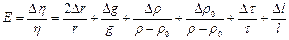
т.к. 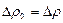, то

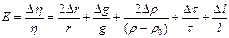
Подставляя численные значения, получим:

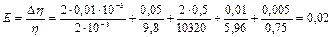
В процентах относительная погрешность составляет:

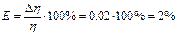
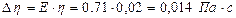Максимально возможная абсолютная погрешность в определении h равна:

Результат измерений:

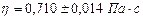
5. Максимальная абсолютная погрешность прямых измерений определяется так, как это показано в параграфе 2. Если некоторая величина измеряется электроизмерительным прибором, то абсолютная погрешность определяется выражением Dx=g×x_H, где g - класс точности прибора; x_н - номинальное значение прибора (см. параграф 12).

В некоторых случаях используется для оценки прямого измерения предельная погрешность, которая равна половине цены деления прибора. Если в пределах одного деления отсчет затруднителен, то предельная погрешность равна цене деления прибора.

Например, при измерении температуры термометром с ценой деления 0,1^о С Dt = 0,05^о С, если шкала сжата, то Dt = 0,1^о С. Если в работе даются значения некоторых величин, измеренных заранее, то погрешность принимается равной ее предельной величине, т.е. равной половине единицы наименьшего разряда, представленного в числе. Например, если дана масса тела

m= 125,40 г, то Dm = 0,05 г; m = (125,40 ± 0,05) г.

4. Графическое изображение результатов измерений

Во многих случаях свойства функций становятся более ясными и наглядными, если эту функцию изобразить графически, т.е. построить ее график. Именно поэтому часто возникает необходимость изобразить графически физические величины, являющиеся функцией одной или двух переменных. Для этого обычно используют прямоугольную систему координат, в некоторых случаях прибегают и к другим системам координат, например, полярной.

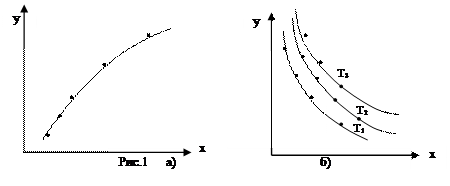
Чтобы графически изобразить соответствующую зависимость, наносят на ось абсцисс шкалу значений аргумента, а на ось ординат - шкалу значений функции. Результаты измерений, т.е. соответствующие пары значений аргумента (x) и функции (y), наносят на координатную плоскость в виде точек, а затем эти точки соединяют плавной линией. Из-за наличия неизбежных ошибок измерений не удается соединить плавной линией все точки. Поэтому проводят усредненную прямую или кривую. Степень отклонения экспериментальных значений (точек) от проведенной усредненной прямой или кривой характеризует погрешность измерений (см. рис. 1а). Если физическая величина является функцией двух переменных, то прибегают к построению семейства кривых, а одной из величин в этом случае придают ряд постоянных значений. Например, зависимость давления для данной массы газа от объема при фиксированных температурах Т₁, Т₂,... Т_n (рис. 1 б).

График должен вычерчиваться на миллиметровой бумаге. При выборе масштаба графика необходимо иметь в виду следующее:

1.Наименьшее расстояние, которое может быть отсчитано по графику, должно быть не меньше абсолютной ошибки измерения.

2.За начало отсчета координат не обязательно принимать нулевые значения измеренных величин. Если измеренные значения физических величин заключены в интервалах V₀-V P₀ - P, то начало отсчета можно совместить со значениями, близкими к V₀ и P₀.

3.При построении графиков используется равномерный, полулогарифмический и логарифмический масштабы.

В первом случае по обеим осям откладывается равномерный масштаб. Во втором случае по одной оси откладывается равномерный масштаб, а по другой - масштаб, пропорциональный логарифму натуральных чисел. В третьем случае логарифмический масштаб наносится на обеих осях координат. Например, зависимость типа 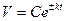(С - const; k - const) удобно изображать в полулогарифмическом масштабе, а зависимость типа xⁿy^k = const - в логарифмическом масштабе.

Дата добавления: 2014-01-04