Теория метода. Движения. Дать определения момента инерции, момента силы

ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ МАЯТНИКА МАКСВЕЛЛА

Движения. Дать определения момента инерции, момента силы.

Напишите и сформулируйте основной закон динамики вращательного

2. Получить рабочую формулу (5).

3. Как определить момент инерции крестовины не снимая с нее грузов?

4. При любом ли расположении грузов на крестовине их можно считать

точечными?

Л а б о р а т о р н а я р а б о т а № 9

Ц е л ь р а б о т ы: научиться составлять уравнения для поступатель-ного и вращательного видов движения

П р и б о р ы: маятник Максвелла, штангенциркуль.

Маятник Максвелла представляет собой массивный диск (1) жёстко посаженный на вал (2). Концы вала подвешены на нитях (3) одинаковой длины. Если намотать нити на вал, то маятник поднимется на некоторую высоту h. При отключении электромагнита вал, вращаясь вместе с диском, будет опускаться, а нити будут разматываться. Достигнув нижнего положения, система поднимается вверх, наматывая нити в обратную сторону. Удерживают маятник в верхнем положении электро-

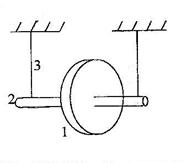рис. 1.

магнитом, притягивающий стальной ободок туго надетый на дюралевый диск. При выключении электромагнита маятник, разматывая нити опускается вниз и одновременно включает секундомер, который срабатывает при попадании луча на фотоэлемент. При достижении нижней точки маятник закрывает луч другого фотоэлемента и останавливает секундомер.

На маятник действуют две силы: сила тяжести F_T, направленная вертикально вниз и сила упругости двух нитей 2Т (рис.2).

Напишем второй закон Ньютона для поступательного и вращательного движения применительно к маятнику Максвелла.

F_T – 2Т = ma (1)

М = J ε (2)

где М – момент сил, J - момент инерции ε - угловое ускорение. Момент силы по определению равен произведению силы на плечо и мы вправе написать М = 2Т r (3) где r – радиус вала., на которую наматывается нить. Объединяя формулы (2) и (3) имеем 2Т r = J ε (4)

Из формулы (1) найдем 2Т

2Т = F_T – ma = mg – ma = m(g-a) (5)

Подставляя в формулу (4) значение 2Т имеем

m(g-a)r = J ε (6)

Используя связь между линейным и угловым ускорениями a = r ε откуда 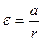подставляя значение ε в уравнение (6) получим

m(g-a) r = 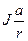r или m (g-a) r² = J a (7)

Из этого уравнения найдём момент инерции маятника J

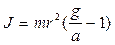(8)

Пройденный путь при равноускоренном движении определяется из уравнения s = υ₀ t +

Пройденный путь равен длине нити или высоте h. Учитывая, что начальная скорость υ₀ = 0 имеем 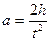(9)

Подставляя значение ускорения в уравнение (7) найдём окончательное выражение для момента инерции маятника Максвелла

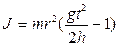(10)

С энергетической точки зрения колебания маятника Максвелла в вертикальной плоскости происходят в результате перехода потенциальной энергии маятника Е_п = mgh в кинетическую энергию поступательного и вращательного движения Е_к + Е_вр. = +

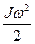
и наоборот.

В данной работе также определяют силу сопротивления, исходя из закона сохранения энергии следующим образом: если считать, что первоначально маятник находился на высоте h₁, а спустя период поднялся на высоту h₂ (h₂ < h₁ из-за сил сопротивления движению), то изменение потенциальной энергии будет равна работе сил сопротивления: mgh₁- mgh₂ = F_c(h₁+ h₂)

Отсюда найдем 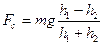(11)

Дата добавления: 2014-01-04