Тема 11. Элементы квантовой механики

Французский ученый Луи де Бройль в 1923 году выдвинул гипотезу об универсальности корпускулярно-волнового дуализма, т.е. не только фотоны, но и электроны и любые другие частицы наряду с корпускулярными обладают также волновыми свойствами.

Количественные соотношения, связывающие корпускулярные и волновые свойства частиц

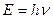и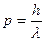

Таким образом, любой частице, обладающей импульсом, сопоставляют волновой процесс с длиной волны

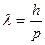- формула волны де-Бройля

На частицы вещества переносится также связь между полной энергией частицы Е и ν волн де Бройля.

Но тогда волновые свойства должны быть присущи и макроскопическим телам. Например, частице массой 1 г, движущейся со скоростью 1 м/с соответствует волна де Бройля λ= 10^-28 м. Такая длина волны лежит за пределами доступной наблюдению области. Поэтому считается, что макроскопические тела проявляют только корпускулярные свойства.

Рассмотрим свойства волн де Бройля. Пусть частица массой m движется со скоростью υ.

Фазовая скорость – скорость перемещения фазы волны

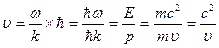
где 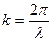– волновое число; ω – циклическая частота волны.

Групповая скорость - скорость движения группы волн, образующих в каждый момент времени в пространстве волновой пакет

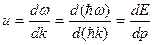
Для свободной частицы

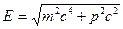
Тогда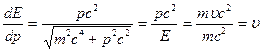

Таким образом, групповая скорость волн де Бройля равна скорости частицы.

Групповая скорость фотона

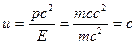
равна скорости самого фотона.

Согласно двойственной корпускулярно-волновой природе микрочастиц, используются то волновые, то корпускулярные представления. Поэтому необходимы некоторые ограничения в применении к объектам микромира понятий классической механики.

В классической механике всякая частица движется по определенной траектории, поэтому в любой момент времени фиксированы ее координата и импульс. В случае микрочастиц этого сказать нельзя, это следует из корпускулярно-волнового дуализма. То есть нельзя говорить о движении микрочастицы по определенной траектории и точных значениях ее координаты и импульса.

Таким образом, микрочастица не может иметь одновременно определенную координату (x, y, z) и определенную соответствующую проекцию импульса (p_x, p_y, p_z), причем неопределенности этих величин удовлетворяют условиям

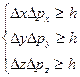- соотношение неопределенностей Гейзенберга

Соотношение неопределенностей Гейзенберга – квантовое ограничение применимости классической механики к микрообъектам.

Из гипотезы де Бройля и соотношения неопределенностей вытекает, что уравнением движения в квантовой механике, описывающим движение микрочастиц в различных силовых полях, должно быть уравнение, из которого вытекали бы волновые свойства частиц. Следовательно, это уравнение должно быть волновым.

Это уравнение было сформулировано Шредингером и имеет вид

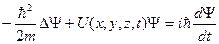- уравнение Шредингера

где 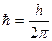- постоянная Планка, m – масса частицы,

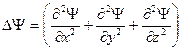- оператор Лапласа, i – мнимая единица,

U (x, y,z,t) - потенциальная энергия частицы,

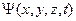- волновая функция частицы.

Уравнение Шредингера для стационарных состояний

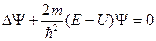
где Е – полная энергия частицы, в случае стационарного поля постоянная.

Тема 12. Теория атома водорода по Бору

Существуют две модели атома – Томсона и Резерфорда.

Модель Томсона: атом представляют как кекс, начиненный изюмом – электроны. Атом представляет непрерывно заряженный «+» зарядом шар радиусом 10^-10м, внутри которого около своих положений колеблются электроны. Суммарный «-» заряд электронов равен «+» заряду шара, поэтому атом в целом нейтрален.

В 1911 году Резерфорд предложил ядерную (планетарную) модель атома.

е

е Вся масса атома сосредоточена в ядре, имеющего

е е заряд Ze. Так как атомы нейтральны, то заряд

е е ядра равен суммарному заряду электронов, т.е.

е е вокруг ядра должно вращаться Z электронов.

Но существует два противоречия:

1) Электрон движется вокруг ядра по круговой орбите радиусом R..

II – закон Ньютона для электрона, движущегося по окружности под действием кулоновской силы

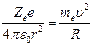
В уравнении два неизвестных R и u, следовательно, существует бесчисленное множество значений R и соответствующих ему значений u. Поэтому величины R и u могут меняться непрерывно, т.е. испускается любая, а не вполне определенная порция энергии. Тогда спектры атомов должны быть сплошными. В действительности, опыт показывает, что атомы имеют линейчатый спектр.

2) Согласно электродинамике, ускоренно движущиеся электроны, должны излучать электромагнитные волны и вследствие этого терять энергию. В результате электроны будут приближаться к ядру и в конце концов упадут на него. Таким, образом, атом Резерфорда оказывается неустойчивой системой – что опять противоречит действительности.

Преодоление этих трудностей потребовало создания новой квантовой теории атома.

Исследования спектров излучения отдельных атомов показали, что каждому газу присущ определенный линейчатый спектр, состоящий из отдельных близко расположенных спектральных линий.

Самым изученным является спектр атома водорода.

Эмпирическая формула, описывающая все известные в то время спектральные линии атома водорода в видимой области спектра

серия Бальмера 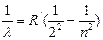n = 3,4,5 …

где R¢ = 1,1×10^-7 м ^-1 – постоянная Ридберга

Так, как 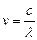, то для частоты

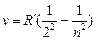n = 3,4,5 …

R = R¢× c = 3,29×10¹⁵ c ^-1 – постоянная Ридберга.

Спектральные линии с различными n образуют группу или серию линий – серия Бальмера.

С увеличением n линии сближаются; n» ¥ - определяет границу серии, к которой со стороны больших частот примыкает сплошной спектр.

В спектре атома водорода было обнаружено еще несколько серий.

В ультрафиолетовой области спектра находится

серия Лаймана 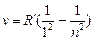n = 2,3,4 …

В инфракрасной области были обнаружены

серия Пашена 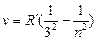n = 4,5,6 …

серия Брэкета 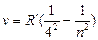n = 5,6,7 …

серия Пфунда 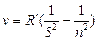n = 6,7,8 …

серия Хэмфри 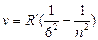n = 7,8,9 …

Все эти серии можно выразить одной формулой

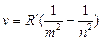- обобщенная формула Бальмера

m = 1,2, 3,… - определяет серию.

Первая попытка построить квантовую теорию атома в 1913 году предпринята датским физиком Н. Бором. В основу своей теории положил два постулата.

I постулат Бора - постулат стационарных состояний: в атоме существуют такие стационарные состояния, в котором он не излучает энергии. Стационарным состояниям соответствуют стационарные орбиты, по которым движутся электроны. Движение электронов по стационарным орбитам не сопровождается излучением электромагнитных волн.

II постулат Бора - правило частот: при переходе электрона с одной стационарной орбиты на другую излучается (поглощается) один фотон с энергией

hn = E_n – E_m

равной разности энергии соответствующих стационарных состояний

- определяет линейчатый спектр атома

При E_m < E_n – излучение фотона - переход электрона с более удаленной от ядра орбиты на более близлежащую.

При E_m > E_n – поглощение фотона - переход электрона на более удаленную от ядра орбиту.

Французский ученый Луи де Бройль в 1924 году выдвинул гипотезу об универсальности корпускулярно-волнового дуализма. Де Бройль утверждал, что не только фотоны, но электроны и любые другие частицы материи наряду с корпускулярными - энергия и импульс, обладают также волновыми свойствами - частота и длина волны.

Для фотонов связь между корпускулярными и волновыми свойствами частиц

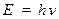
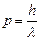
Смелость гипотезы заключается в том, что это соотношение постулировалось не только для фотонов, но и для других микрочастиц, которые обладают массой покоя.

Таким образом, любой частице, обладающей импульсом, сопоставляют волну, длина которой вычисляется по формуле де Бройля

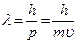- длина волны де Бройля

где 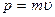- импульс частицы.

Но тогда волновые свойства де Бройля присущи и макроскопическим телам, но они не обнаружены.

Например, частице массой 1 г, движущейся со скоростью 1 м/с, соответствует волна де Бройля l= 1^{-2 м.} Такая длина волны лежит за пределами доступной наблюдению области, поэтому считается, что макроскопические тела проявляют только корпускулярные свойства.

Кроме того, на частицы вещества переносится связь между полной энергией частицы Е и частотой n волн де Бройля.

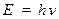- универсальное соотношение, справедливо как

для фотонов, так и для любых микрочастиц.

Фазовая и групповая скорости волн де Бройля:

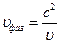- фазовая скорость

- групповая скорость

Для свободной частицы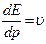

Таким образом, групповая скорость волн де Бройля равна скорости частицы.

Согласно корпускулярно-волновой природе частиц вещества, для описания микрочастиц используются то волновые, то корпускулярные представления. Приписывать все свойства частиц и свойства волн нельзя.

В классической механике всякая частица движется по определенной траектории, так, что в любой момент времени точно фиксированы ее координата и импульс. О движении микрочастицы по определенной траектории и точных значениях координаты и импульса говорить нельзя из-за наличия волновых свойств.

Согласно соотношению неопределенностей Гейзенберга, микрочастица не может иметь одновременно и определенную координату (x,y,z) и определенную соответствующую проекцию импульса (р_х, р_y, р_z,)

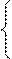
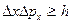
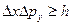
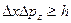
т.е. произведение неопределенностей координаты и соответствующей ей проекции импульса не может быть меньше величины порядка h.

Таким образом, соотношение неопределенностей является квантовым ограничением применимости классической механики к микрообъектам.

В квантовой механике состояние микрочастиц описывается с помощью волновой функции, которая является основным носителем информации об их корпускулярных и волновых свойствах.

Основное уравнение в квантовой механике сформулировано Шредингером.

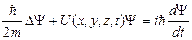- общее уравнение Шредингера

где 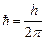- постоянная Планка, m – масса частицы

D Y - оператор Лапласа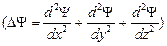

i – мнимая единица

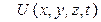- потенциальная функция частицы в силовом поле, в котором

она движется

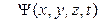- искомая волновая функция частицы.

Уравнение Шредингера справедливо для любой частицы, движущейся со скоростью u<<c.

Уравнение Шредингера для стационарных состояний имеет вид

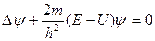
Е – полная энергия частицы.

Дата добавления: 2014-01-04